
【题目】如图,在等腰△ABC中,CH是底边上的高线,点P是线段CH上不与端点重合的任意一点,连接AP交BC于点E,连接BP交AC于点F. 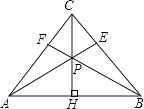
(1)证明:∠CAE=∠CBF;
(2)证明:AE=BF.
【答案】
(1)证明:在等腰△ABC中,
∵CH是底边上的高线,
∴∠ACH=∠BCH,
在△ACP和△BCP中, 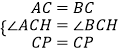 ,
,
∴△ACP≌△BCP(SAS),
∴∠CAE=∠CBF(全等三角形对应角相等)
(2)在△AEC和△BFC中 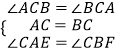 ,
,
∴△AEC≌△BFC(ASA),
∴AE=BF(全等三角形对应边相等).
【解析】(1)根据等腰三角形三线合一的性质可得CH平分∠ACB,再证明△ACE和△BCF全等,然后根据全等三角形对应角相等可得结论;(2)证明△AEC≌△BFC,根据全等三角形对应边相等即可证明.
【考点精析】本题主要考查了等腰三角形的性质的相关知识点,需要掌握等腰三角形的两个底角相等(简称:等边对等角)才能正确解答此题.


 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案科目:初中数学 来源: 题型:
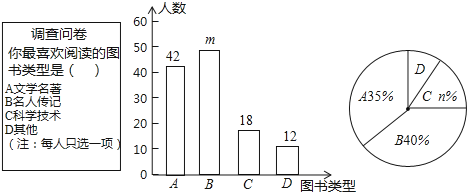
【题目】为了培养学生的阅读习惯,某校开展了“读好书,助成长”系列活动,并准备购置一批图书,购书前 ,对学生喜欢阅读的图书类型进行了抽样调查,并将调查数据绘制成两幅不完整的统计图,如图所示,根据统计图所提供的信息,回答下列问题:
(1)本次调查共抽查了 名学生,两幅统计图中的m= ,n= .
(2)已知该校共有960名学生,请估计该校喜欢阅读“A”类图书的学生约有多少人?
(3)学校要举办读书知识竞赛,七年(1)班要在班级优胜者2男1女中随机选送2人参赛,求选送的两名参赛学生为1男1女的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,方格纸中每个小方格都是边长为1的正方形,我们把以格点连线为边的多边形称为“格点多边形”.如图(一)中四边形ABCD就是一个“格点四边形”. 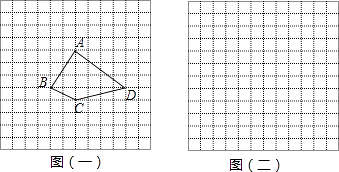
(1)作出四边形ABCD关于直线BD对称的四边形A′B′C′D′;
(2)求图(一)中四边形ABCD的面积;
(3)在图(二)方格纸中画一个格点三角形EFG,使△EFG的面积等于四边形ABCD的面积且△EFG为轴对称图形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在⊙O中,直径AB⊥CD,垂足为E,点M在OC上,AM的延长线交⊙O于点G,交过C的直线于F,∠1=∠2,连结CB与DG交于点N.
(1)求证:CF是⊙O的切线;
(2)求证:△ACM∽△DCN;
(3)若点M是CO的中点,⊙O的半径为4,cos∠BOC=![]() ,求BN的长.
,求BN的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近年来,随着社会竞争的日益激烈,家长为使孩子不输在教育的起跑线上,不惜花费重金购置教育质量好的学区的房产.张先生准备购买一套小户型学区房,他去某楼盘了解情况得知,该户型的单价是12000元/m2 , 面积如图所示(单位:米,卫生间的宽未定,设宽为x米),售房部为张先生提供了以下两种优惠方案: 方案一:整套房的单价是12000元/m2 , 其中厨房可免费赠送 ![]() 的面积;
的面积;
方案二:整套房按原销售总金额的9折出售.
(1)用y1表示方案一中购买一套该户型商品房的总金额,用y2表示方案二中购买一套该户型商品房的总金额,分别求出两种方案中的总金额y1、y2(用含x的式子表示);
(2)求当x=2时,两种方案的总金额分别是多少元?
(3)张先生因现金不够,在银行借了18万元住房贷款,贷款期限为6年,从开始贷款的下一个月起逐月偿还,贷款月利率是0.5%,每月还款数额=平均每月应还的贷款本金数额+月利息,月利息=上月所剩贷款本金数额×月利率. ①张先生借款后第一个月应还款数额是多少元?
②假设贷款月利率不变,若张先生在借款后第n(1≤n≤72,n是正整数)个月的还款数额为P,请写出P与n之间的关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个三角形的第一条边长为a+2b,第二条边比第一条边短b-2,第三条边比第二条边短3.
(1)请用a、b的式子表示此三角形的周长;
(2)当a=2,b=3时,求此三角形的周长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com