
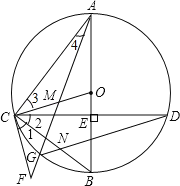
【题目】如图,在⊙O中,直径AB⊥CD,垂足为E,点M在OC上,AM的延长线交⊙O于点G,交过C的直线于F,∠1=∠2,连结CB与DG交于点N.
(1)求证:CF是⊙O的切线;
(2)求证:△ACM∽△DCN;
(3)若点M是CO的中点,⊙O的半径为4,cos∠BOC=![]() ,求BN的长.
,求BN的长.

【答案】(1)证明见解析;(2)证明见解析;(3)BN=![]() .
.
【解析】试题分析:(1)、根据BO=CO得出∠B=∠BCO,根据∠2+∠B=90°,∠1=∠2得出∠1+∠BCO=90°,从而得到切线;(2)、根据AB为直径得到∠ACB=∠FCO=90°,从而得出∠3=∠1,即∠3=∠2,结合∠4=∠D得出三角形相似;(3)、根据题意得出BE和AE的长度,然后根据勾股定理得出CE、AC和BC的长度,最后根据△ACM∽△DCN得出CN的长度,从而根据BN=BC-CN得出答案.
试题解析:(1)、∵△BCO中,BO=CO, ∴∠B=∠BCO,
在△BCE中,∠2+∠B=90°, 又∵∠1=∠2, ∴∠1+∠BCO=90°, 即∠FCO=90°,
∴CF是⊙O的切线;
(2)∵AB是⊙O直径, ∴∠ACB=∠FCO=90°, ∴∠ACB﹣∠BCO=∠FCO﹣∠BCO,
即∠3=∠1, ∴∠3=∠2,∵∠4=∠D, ∴△ACM∽△DCN;
(3)∵⊙O的半径为4,即AO=CO=BO=4, 在△COE中,∠BOC=![]() ,
,
∴OE=CO∠BOC=4×=1,
由此可得:BE=3,AE=5,由勾股定理可得:CE=![]() =
=![]() =
=![]() ,
,
AC=![]() =
=![]() =2
=2![]() , BC=
, BC=![]() =
=![]() =2
=2![]() ,
,
∵AB是⊙O直径,AB⊥CD, ∴由垂径定理得:CD=2CE=2![]() ,
,
∵△ACM∽△DCN, ∴![]() =
=![]() , ∵点M是CO的中点,CM=AO=×4=2,
, ∵点M是CO的中点,CM=AO=×4=2,
∴CN=![]() =
=![]() =
=![]() , ∴BN=BC﹣CN=2
, ∴BN=BC﹣CN=2![]() ﹣
﹣![]() =
=![]() .
.


 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案科目:初中数学 来源: 题型:
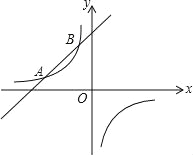
【题目】如图,已知反比例函数y1=![]() (k≠0)的图象经过点(8,-
(k≠0)的图象经过点(8,-![]() ),直线y2=x+b与反比例函数图象相交于点A和点B(m,4).
),直线y2=x+b与反比例函数图象相交于点A和点B(m,4).
(1)求上述反比例函数和直线的解析式;
(2)当y1<y2时,请直接写出x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明所在城市的“阶梯水价”收费办法是:每户用水不超过5吨,每吨水费x元;超过5吨,每吨加收2元,小明家今年5月份用水9吨,共交水费为44元,根据题意列出关于x的方程正确的是( )
A.5x+4(x+2)=44
B.5x+4(x﹣2)=44
C.9(x+2)=44
D.9(x+2)﹣4×2=44
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若点A(2,﹣2),B(﹣1,﹣2),则直线AB与x轴和y轴的位置关系分别是( )
A.相交,相交
B.平行,平行
C.平行,垂直相交
D.垂直相交,平行
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰△ABC中,CH是底边上的高线,点P是线段CH上不与端点重合的任意一点,连接AP交BC于点E,连接BP交AC于点F. 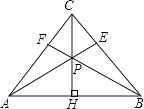
(1)证明:∠CAE=∠CBF;
(2)证明:AE=BF.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com