
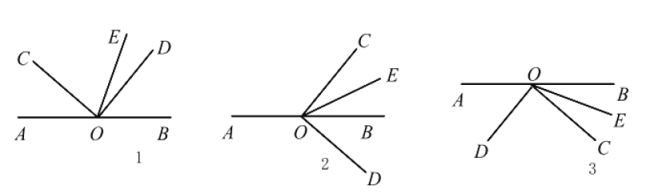
【题目】如图 1,![]() 是直线
是直线![]() 上的一点,
上的一点,![]() 是直角,
是直角,![]() 平分
平分![]() .
.
(1)若![]() ,则
,则![]() 的度数为 °;
的度数为 °;
(2)将图 1 中的![]() 绕顶点
绕顶点 ![]() 顺时针旋转至图 2 的位置,其他条件不变, 探究
顺时针旋转至图 2 的位置,其他条件不变, 探究![]() 和
和![]() 的度数之间的关系,写出你的结论,并说明理由;
的度数之间的关系,写出你的结论,并说明理由;
(3)将图 1 中的![]() 绕顶点
绕顶点 ![]() 顺时针旋转至图 3 的位置,其他条件不变,直接写出
顺时针旋转至图 3 的位置,其他条件不变,直接写出![]() 和
和![]() 的度数之间的关系: .
的度数之间的关系: .
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案科目:初中数学 来源: 题型:
【题目】某公司购买了一批A、B型芯片,其中A型芯片的单价比B型芯片的单价少9元,已知该公司用3120元购买A型芯片的条数与用4200元购买B型芯片的条数相等.
(1)求该公司购买的A、B型花片的单价各是多少元?
(2)若两种芯片共购买了200条,且购买的总费用不超过6300元,求A型芯片至少购买多少条?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现有正方形ABCD和一个以O为直角顶点的三角板,移动三角板,使三角板的两直角边所在直线分别与直线BC,CD交于点M,N.
(1)如图1,若点O与点A重合,则OM与ON的数量关系是__________________;
(2)如图2,若点O在正方形的中心(即两对角线的交点),则(1)中的结论是否仍然成立?请说明理由;
(3)如图3,若点O在正方形的内部(含边界),当OM=ON时,请探究点O在移动过程中可形成什么图形?
(4)如图4是点O在正方形外部的一种情况.当OM=ON时,请你就“点O的位置在各种情况下(含外部)移动所形成的图形”提出一个正确的结论.(不必说理)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,欢欢和乐乐分别站在正方形![]() 的顶点
的顶点![]() 和顶点
和顶点![]() 处,欢欢以
处,欢欢以![]() 的速度走向终点
的速度走向终点![]() ,途中位置记为点
,途中位置记为点![]() ;乐乐以
;乐乐以![]() 的速度走向终点
的速度走向终点![]() ,途中位置记为
,途中位置记为![]() .假设两人同时出发,两人都到达终点时结束运动.已知正方形边长为
.假设两人同时出发,两人都到达终点时结束运动.已知正方形边长为![]() ,点
,点![]() 在
在![]() 上,
上,![]() .记三角形
.记三角形![]() 的面积为
的面积为![]() ,三角形
,三角形![]() 的面积为
的面积为![]() .设出发时间为
.设出发时间为![]() :
:
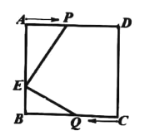
(1)如图情况,用含![]() 的代数式表示下列线段的长度:
的代数式表示下列线段的长度:
![]() ______;
______;![]() ______;
______; ![]() ______;
______;![]() ______;
______;
(2)如图情况,他们出发多少秒后![]() ?
?
(3)是否存在这样的时刻![]() ,使得
,使得![]() ?若存在,请求出
?若存在,请求出![]() 的最小值,若不存在,请说明理由.
的最小值,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,两个直角三角形的直角顶点重合,∠AOC=40°,求∠BOD 的度数.
结合图形,完成填空:
解法 1:
因为![]() ,
,![]()
所以![]()
![]()
因为![]()
![]()
所以![]()
![]()
![]()
所以![]()
![]()
解法2:
因为![]()
![]() ,
,![]()
![]() ,①
,①
所以![]() .②
.②
因为![]()
所以![]()
![]()
在上面①到②的推导过程中,理由依据是: .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在坐标平面内△ABC的顶点坐标分别为A(0,2),B(3,3),C(2,1),(正方形网格中,每个小正方形的边长是1个单位长度)
(1)画出△ABC关于原点对称的△A1B1C1,并直接写出点C1点的坐标;
(2)画出△ABC绕点A顺时针方向旋转90°后得到的△A2B2C2,并直接写出C2点的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市要销售一种新上市的文具,进价为20元,试营销阶段发现:当销售单价是25元时,每天的销售量为250件,销售单价每上涨1元,每天的销售量就减少10件.
(1)求销售单价为多少元时,该文具每天的销售利润最大,并求出最大的利润;
(2)经过试营销后,超市按(1)中单价销售,为了回馈广大顾客,同时提高该文具知名度,超市决定在1月1日当天开展降价促销活动,若每件文具降价2a%,则可多售出4a%,结果当天销售额为5670元,要使销量尽可能地大,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点D是直线![]() 外一点,在
外一点,在![]() 上取两点A,B,连接AD,分别以点B,D为圆心,AD,AB的长为半径画弧,两弧交于点C,连接CD,BC,则四边形ABCD是平行四边形,理由是:_________________________
上取两点A,B,连接AD,分别以点B,D为圆心,AD,AB的长为半径画弧,两弧交于点C,连接CD,BC,则四边形ABCD是平行四边形,理由是:_________________________
 .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学课上, 老师要求同学们利用三角板画两条平行线.老师说苗苗和小华两位同学画法都是正确的,两位同学的画法如下:
苗苗的画法:

①将含30°角的三角尺的最长边与直线a重合,另一块三角尺最长边与含30°角的三角尺的最短边紧贴;
②将含30°角的三角尺沿贴合边平移一段距离,画出最长边所在直线b,则b//a.
小华的画法:

①将含30°角三角尺的最长边与直线a重合,用虚线做出一条最短边所在直线;
②再次将含30°角三角尺的最短边与虚线重合,画出最长边所在直线b,则b//a.
请在苗苗和小华两位同学画平行线的方法中选出你喜欢的一种,并写出这种画图的依据.
答:我喜欢__________同学的画法,画图的依据是__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com