
【题目】某公司购买了一批A、B型芯片,其中A型芯片的单价比B型芯片的单价少9元,已知该公司用3120元购买A型芯片的条数与用4200元购买B型芯片的条数相等.
(1)求该公司购买的A、B型花片的单价各是多少元?
(2)若两种芯片共购买了200条,且购买的总费用不超过6300元,求A型芯片至少购买多少条?
【答案】(1)A型芯片的单价为26元/条,B型芯片的单价为35元/条;(2)A型芯片至少购买78条
【解析】
(1)设B型芯片的单价为x元/条,则A型芯片的单价为(x﹣9)元/条,根据数量=总价÷单价结合用3120元购买A型芯片的条数与用4200元购买B型芯片的条数相等,即可得出关于x的分式方程,解之经检验后即可得出结论;
(2)设购买a条A型芯片,则购买(200﹣a)条B型芯片,根据总价=单价×数量,即可得出关于a的一元一次方程,解之即可得出结论.
(1)设B型芯片的单价为x元/条,则A型芯片的单价为(x﹣9)元/条,
根据题意得:![]() ,
,
解得:x=35,
经检验,x=35是原方程的解,且符合题意,
∴x﹣9=26.
答:A型芯片的单价为26元/条,B型芯片的单价为35元/条.
(2)设购买a条A型芯片,则购买(200﹣a)条B型芯片,
根据题意得:26a+35(200﹣a)≤6300,
解得:a≥![]() .
.
答:A型芯片至少购买78条.


科目:初中数学 来源: 题型:
【题目】如图,直线y=x+m与y=nx+4n(n≠0)的交点的横坐标为2,则关于x的不等式x+m>nx+4n>0的整数解为 ( )

A. 1B. 3C. 4D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】端午节“赛龙舟,吃粽子”是中华民族的传统习俗.节日期间,小邱家包了三种不同馅的粽子,分别是:红枣粽子(记为A),豆沙粽子(记为B),肉粽子(记为C),这些粽子除了馅不同,其余均相同.粽子煮好后,小邱的妈妈给一个白盘中放入了两个红枣粽子,一个豆沙粽子和一个肉粽子;给一个花盘中放入了两个肉粽子,一个红枣粽子和一个豆沙粽子.
根据以上情况,请你回答下列问题:
(1)假设小邱从白盘中随机取一个粽子,恰好取到红枣粽子的概率是多少?
(2)若小邱先从白盘里的四个粽子中随机取一个粽子,再从花盘里的四个粽子中随机取一个粽子,请用列表法或画树状图的方法,求小邱取到的两个粽子中一个是红枣粽子、一个是豆沙粽子的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形纸片ABCD中,已知AD =8,折叠纸片使AB边与对角线AC
重合,点B落在点F处,折痕为AE,且EF=3,则AB的长为( )

A. 3 B. 4
C. 5 D. 6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,过平行四边形ABCD对角线交点O的线段EF,分别交AD,BC于点E,F,当AE=ED时,△AOE的面积为4,则四边形EFCD的面积是( )
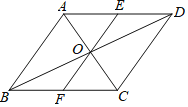
A.8B.12C.16D.32
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,点H是BC的中点,作射线AH,在线段AH及其延长线上分别取点E,F,连接BE,CF.
(1)如图1,请你添加一个条件_____________,使得△BEH≌△CFH:
(2)如图2,在(1)的条件下,当BH与EH满足什么关系时,四边形BFCE是矩形,并给出证明.


图1 图2
查看答案和解析>>
科目:初中数学 来源: 题型:
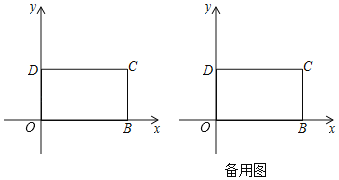
【题目】如图,矩形OBCD中,OB=5,OD=3,以O为原点建立平面直角坐标系,点B,点D分别在x轴,y轴上,点C在第一象限内,若平面内有一动点P,且满足S△POB=![]() S矩形OBCD,问:
S矩形OBCD,问:
(1)当点P在矩形的对角线OC上,求点P的坐标;
(2)当点P到O,B两点的距离之和PO+PB取最小值时,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
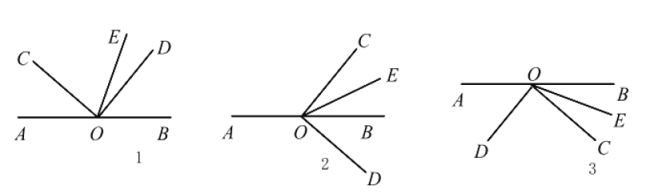
【题目】如图 1,![]() 是直线
是直线![]() 上的一点,
上的一点,![]() 是直角,
是直角,![]() 平分
平分![]() .
.
(1)若![]() ,则
,则![]() 的度数为 °;
的度数为 °;
(2)将图 1 中的![]() 绕顶点
绕顶点 ![]() 顺时针旋转至图 2 的位置,其他条件不变, 探究
顺时针旋转至图 2 的位置,其他条件不变, 探究![]() 和
和![]() 的度数之间的关系,写出你的结论,并说明理由;
的度数之间的关系,写出你的结论,并说明理由;
(3)将图 1 中的![]() 绕顶点
绕顶点 ![]() 顺时针旋转至图 3 的位置,其他条件不变,直接写出
顺时针旋转至图 3 的位置,其他条件不变,直接写出![]() 和
和![]() 的度数之间的关系: .
的度数之间的关系: .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com