
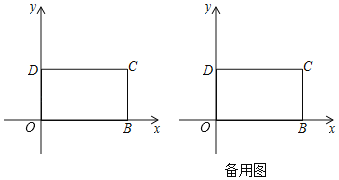
【题目】如图,矩形OBCD中,OB=5,OD=3,以O为原点建立平面直角坐标系,点B,点D分别在x轴,y轴上,点C在第一象限内,若平面内有一动点P,且满足S△POB=![]() S矩形OBCD,问:
S矩形OBCD,问:
(1)当点P在矩形的对角线OC上,求点P的坐标;
(2)当点P到O,B两点的距离之和PO+PB取最小值时,求点P的坐标.
【答案】(1)P(![]() ,2);(2)(
,2);(2)(![]() ,2)或(﹣
,2)或(﹣![]() ,2)
,2)
【解析】
(1)根据已知条件得到C(5,3),设直线OC的解析式为y=kx,求得直线OC的解析式为y=![]() x,设P(m,
x,设P(m,![]() m),根据S△POB=
m),根据S△POB=![]() S矩形OBCD,列方程即可得到结论;
S矩形OBCD,列方程即可得到结论;
(2)设点P的纵坐标为h,得到点P在直线y=2或y=﹣2的直线上,作B关于直线y=2的对称点E,则点E的坐标为(5,4),连接OE交直线y=2于P,则此时PO+PB的值最小,设直线OE的解析式为y=nx,于是得到结论.
(1)如图:
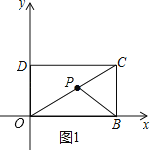
∵矩形OBCD中,OB=5,OD=3,
∴C(5,3),
设直线OC的解析式为y=kx,
∴3=5k,
∴k=![]() ,
,
∴直线OC的解析式为y=![]() x,
x,
∵点P在矩形的对角线OC上,
∴设P(m,![]() m),
m),
∵S△POB=![]() S矩形OBCD,
S矩形OBCD,
∴![]() 5×
5×![]() m=
m=![]() 3×5,
3×5,
∴m=![]() ,
,
∴P(![]() ,2);
,2);
(2)∵S△POB=![]() S矩形OBCD,
S矩形OBCD,
∴设点P的纵坐标为h,
∴![]() h×5=
h×5=![]() 5,
5,
∴h=2,
∴点P在直线y=2或y=﹣2上,
作B关于直线y=2的对称点E,
则点E的坐标为(5,4),
连接OE交直线y=2于P,则此时PO+PB的值最小,
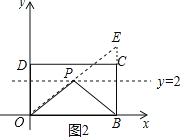
设直线OE的解析式为y=nx,
∴4=5n,
∴n=![]() ,
,
∴直线OE的解析式为y=![]() x,
x,
当y=2时,x=![]() ,
,
∴P(![]() ,2),
,2),
同理,点P在直线y=﹣2上,
P(![]() ,﹣2),
,﹣2),
∴点P的坐标为(![]() ,2)或(﹣
,2)或(﹣![]() ,2).
,2).


科目:初中数学 来源: 题型:
【题目】已知:如图,在菱形ABCD中,对角线AC、BD相交于点O,DE∥AC,AE∥BD.
(1)求证:四边形AODE是矩形;
(2)若AB=4,∠BCD=120°,求四边形AODE的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司购买了一批A、B型芯片,其中A型芯片的单价比B型芯片的单价少9元,已知该公司用3120元购买A型芯片的条数与用4200元购买B型芯片的条数相等.
(1)求该公司购买的A、B型花片的单价各是多少元?
(2)若两种芯片共购买了200条,且购买的总费用不超过6300元,求A型芯片至少购买多少条?
查看答案和解析>>
科目:初中数学 来源: 题型:
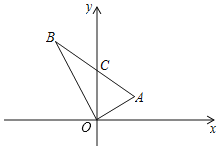
【题目】如图,在平面直角坐标系中,O为原点,点A(2,1),B(﹣2,4),直线AB与y轴交于点C.
(1)求点C的坐标;
(2)求证:△OAB是直角三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“十一”黄金周期间,朱老师织织朋友去某影视城旅游.现有两家旅行社.报价都为![]() 元.且提供服务完全相同.但针对组团游的游客,甲旅行社表示,每人都按八折收费; 乙旅行社表示,若人数不超过
元.且提供服务完全相同.但针对组团游的游客,甲旅行社表示,每人都按八折收费; 乙旅行社表示,若人数不超过![]() 人,每人都按八折收费.若超过
人,每人都按八折收费.若超过![]() 人,則超出部分按七五折收费,假设组团参加甲乙两家旅行社旅游的人数均为
人,則超出部分按七五折收费,假设组团参加甲乙两家旅行社旅游的人数均为![]() 人.
人.
(1)请分别写出甲,乙两家旅行社收取组团游的总费用![]() (元)与
(元)与![]() (人)之间的函数关系式.
(人)之间的函数关系式.
(2)如果朱老师和朋友一共有![]() 人去旅游.那你计算下,在甲、乙两家旅行社中,朱老师应选择哪家?
人去旅游.那你计算下,在甲、乙两家旅行社中,朱老师应选择哪家?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现有正方形ABCD和一个以O为直角顶点的三角板,移动三角板,使三角板的两直角边所在直线分别与直线BC,CD交于点M,N.
(1)如图1,若点O与点A重合,则OM与ON的数量关系是__________________;
(2)如图2,若点O在正方形的中心(即两对角线的交点),则(1)中的结论是否仍然成立?请说明理由;
(3)如图3,若点O在正方形的内部(含边界),当OM=ON时,请探究点O在移动过程中可形成什么图形?
(4)如图4是点O在正方形外部的一种情况.当OM=ON时,请你就“点O的位置在各种情况下(含外部)移动所形成的图形”提出一个正确的结论.(不必说理)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,欢欢和乐乐分别站在正方形![]() 的顶点
的顶点![]() 和顶点
和顶点![]() 处,欢欢以
处,欢欢以![]() 的速度走向终点
的速度走向终点![]() ,途中位置记为点
,途中位置记为点![]() ;乐乐以
;乐乐以![]() 的速度走向终点
的速度走向终点![]() ,途中位置记为
,途中位置记为![]() .假设两人同时出发,两人都到达终点时结束运动.已知正方形边长为
.假设两人同时出发,两人都到达终点时结束运动.已知正方形边长为![]() ,点
,点![]() 在
在![]() 上,
上,![]() .记三角形
.记三角形![]() 的面积为
的面积为![]() ,三角形
,三角形![]() 的面积为
的面积为![]() .设出发时间为
.设出发时间为![]() :
:
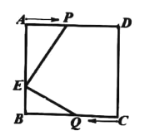
(1)如图情况,用含![]() 的代数式表示下列线段的长度:
的代数式表示下列线段的长度:
![]() ______;
______;![]() ______;
______; ![]() ______;
______;![]() ______;
______;
(2)如图情况,他们出发多少秒后![]() ?
?
(3)是否存在这样的时刻![]() ,使得
,使得![]() ?若存在,请求出
?若存在,请求出![]() 的最小值,若不存在,请说明理由.
的最小值,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点D是直线![]() 外一点,在
外一点,在![]() 上取两点A,B,连接AD,分别以点B,D为圆心,AD,AB的长为半径画弧,两弧交于点C,连接CD,BC,则四边形ABCD是平行四边形,理由是:_________________________
上取两点A,B,连接AD,分别以点B,D为圆心,AD,AB的长为半径画弧,两弧交于点C,连接CD,BC,则四边形ABCD是平行四边形,理由是:_________________________
 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com