
【题目】已知:如图,在菱形ABCD中,对角线AC、BD相交于点O,DE∥AC,AE∥BD.
(1)求证:四边形AODE是矩形;
(2)若AB=4,∠BCD=120°,求四边形AODE的面积.

【答案】(1)详见解析;(2)矩形AODE面积为![]()
【解析】
(1)根据菱形的性质得出AC⊥BD,再根据平行四边形的判定定理得四边形AODE为平行四边形,由矩形的判定定理得出四边形AODE是矩形;
(2)证明△ABC是等边三角形,得出OA=![]() ×4=2,由勾股定理得出OB=2
×4=2,由勾股定理得出OB=2![]() ,由菱形的性质得出OD=OB=2
,由菱形的性质得出OD=OB=2![]() ,即可求出四边形AODE的面积.
,即可求出四边形AODE的面积.
(1)证明:∵DE∥AC,AE∥BD,
∴四边形AODE是平行四边形,
∵在菱形ABCD中,AC⊥BD,
∴平行四边形AODE是矩形,
故四边形AODE是矩形;
(2)解:∵∠BCD=120°,AB∥CD,
∴∠ABC=180°-120°=60°,
∵AB=BC,
∴△ABC是等边三角形,
∴OA=![]() ×4=2,
×4=2,
∵在菱形ABCD中,AC⊥BD
∴由勾股定理OB=![]() =2
=2![]() ,
,
∵四边形ABCD是菱形,
∴OD=OB=2![]() ,
,
∴四边形AODE的面积=OAOD=2![]() =4
=4![]() .
.


科目:初中数学 来源: 题型:
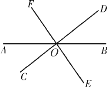
【题目】如图,直线AB,CD,EF相交于点O,则∠AOD的对顶角是_________,∠AOC的邻补角是_______.若∠AOC=50°,则∠BOD=__________,∠COB=______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)先化简,再求值:(2-3x)(-3x-2)-5x(x-1)-(2x-1)2,其中x=-![]() ;
;
(2)已知xy2=-2,求xy(x2y5+3xy3-2y)的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】全国爱眼日是每年的6月6日,2013年世界爱眼日主题确定为“关爱青少年眼健康”,某中学为了解该校学生的视力情况,采用抽样调查的方式,从视力正常、轻度近视、中度近视、重度近视四个方面调查了若干名学生的视力情况,并根据调查结果制作了如下两幅统计图。


根据图中提供的信息解答下列问题:
(1)一共随机调查了多少人?
(2)补全人数统计图;
(3)若该校共有1500名学生,请你估计该校学生视力正常的人数。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠A=52°,∠ABC与∠ACB的角平分线交于D1, ∠ABD1与∠ACD1的角平分线交于点D2,依次类推,∠ABD4与∠ACD4 的角平分线交于点D5,则∠BD5C的度数是( )

A. 56°;B. 60°;C. 68°;D. 94°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】火车匀速通过隧道时,火车在隧道内的长度![]() (米)与火车行驶时间
(米)与火车行驶时间![]() (秒)之间的关系用图象描述如图所示,有下列结论:
(秒)之间的关系用图象描述如图所示,有下列结论:
①火车的长度为120米;
②火车的速度为30米/秒;
③火车整体都在隧道内的时间为25秒;
④隧道长度为750米.
其中正确的结论是_____.(把你认为正确结论的序号都填上)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线CD与直线AB相交于C,根据下列语句画图,并填空.
(1)过点P作PQ∥CD,交AB于点Q(尺规作图);
(2)过点P作PR⊥CD,垂足为R.
(3)在(1)(2)的条件下,若∠ACD=65°,则∠PQB=____度,∠RPQ=____度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC=10,点D是边BC上一动点(不与B,C重合),∠ADE=∠B=α,DE交AC于点E,且cosα=![]() .下列结论:
.下列结论:
①△ADE∽△ACD; ②当BD=6时,△ABD与△DCE全等;
③△DCE为直角三角形时,BD为8; ④0<CE≤6.4.

其中正确的结论是____________.(把你认为正确结论的序号都填上)
查看答案和解析>>
科目:初中数学 来源: 题型:
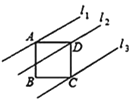
【题目】如图,直线l1,l2,l3分别过正方形ABCD的三个顶点A,D,C,且相互平行,若l1,l2的距离为2,l2,l3的距离为4,则正方形的对角线长为_______________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com