
【题目】“十一”黄金周期间,朱老师织织朋友去某影视城旅游.现有两家旅行社.报价都为![]() 元.且提供服务完全相同.但针对组团游的游客,甲旅行社表示,每人都按八折收费; 乙旅行社表示,若人数不超过
元.且提供服务完全相同.但针对组团游的游客,甲旅行社表示,每人都按八折收费; 乙旅行社表示,若人数不超过![]() 人,每人都按八折收费.若超过
人,每人都按八折收费.若超过![]() 人,則超出部分按七五折收费,假设组团参加甲乙两家旅行社旅游的人数均为
人,則超出部分按七五折收费,假设组团参加甲乙两家旅行社旅游的人数均为![]() 人.
人.
(1)请分别写出甲,乙两家旅行社收取组团游的总费用![]() (元)与
(元)与![]() (人)之间的函数关系式.
(人)之间的函数关系式.
(2)如果朱老师和朋友一共有![]() 人去旅游.那你计算下,在甲、乙两家旅行社中,朱老师应选择哪家?
人去旅游.那你计算下,在甲、乙两家旅行社中,朱老师应选择哪家?
【答案】(1)甲旅行社收取的总费用![]() 与
与![]() 间的函数关系式为:
间的函数关系式为:![]() ;
;
乙旅行社收取的总费用![]() 与
与![]() 间的函数关系式为:
间的函数关系式为: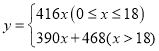 ;
;
(2)朱老师应选择乙旅行社.
【解析】
(1)根据题意,甲旅行社收取的总费用=原价×折扣×人数,人数超过18人时,乙旅行社收取的总费用=前18人总费用+超出人数的费用,可列出函数关系式;
(2)当x=30时,分别计算两旅行社费用,比较可知.
(1)根据题意,甲旅行社收取的总费用![]() 与
与![]() 间的函数关系式为:
间的函数关系式为:
![]() ;
;
当![]() 时,乙旅行社收取的总费用
时,乙旅行社收取的总费用![]() 与
与![]() 间的函数关系式为:
间的函数关系式为:
![]() ;
;
当![]() 时,乙旅行社收取的总费用
时,乙旅行社收取的总费用![]() 与
与![]() 间的函数关系式为:
间的函数关系式为:
![]() ;
;
故乙旅行社收取的总费用![]() 与
与![]() 间的函数关系式为:
间的函数关系式为: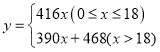 ;
;
(2)当![]() 时,甲旅行社收取的总费用
时,甲旅行社收取的总费用![]() (元),
(元),
乙旅行社收取的总费用![]() (元),
(元),
∵ ![]() ,
,
∴ 朱老师应选择乙旅行社.


 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案科目:初中数学 来源: 题型:
【题目】小明为今年将要参加中考的好友小李制作了一个(如图)正方体礼品盒,六面上各有一字,连起来就是“预祝中考成功”,其中“预”的对面是“中”,“成”的对面是“功”,则它的平面展开图可能是( )

A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,点H是BC的中点,作射线AH,在线段AH及其延长线上分别取点E,F,连接BE,CF.
(1)如图1,请你添加一个条件_____________,使得△BEH≌△CFH:
(2)如图2,在(1)的条件下,当BH与EH满足什么关系时,四边形BFCE是矩形,并给出证明.


图1 图2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将正整数1至2019按一定规律排列如下表:

平移表中带阴影的方框,则方框中五个数的和可以是
A.2010B.2018C.2019D.2020.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形OBCD中,OB=5,OD=3,以O为原点建立平面直角坐标系,点B,点D分别在x轴,y轴上,点C在第一象限内,若平面内有一动点P,且满足S△POB=![]() S矩形OBCD,问:
S矩形OBCD,问:
(1)当点P在矩形的对角线OC上,求点P的坐标;
(2)当点P到O,B两点的距离之和PO+PB取最小值时,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图在数轴上A点表示数a,B点表示数b,AB表示A点和B点之间的距离,且a、b满足|2a+4|+|b-6|=0
![]()
(1)求A,B两点之间的距离;
(2)若在数轴上存在一点C,且AC=2BC,求C点表示的数;
(3)若在原点O处放一个挡板,一个小球甲从点A处以1个单位/秒的速度向左运动;同时另一小球乙从点B处以2个单位/秒的速度也向左运动,在碰到挡板后(忽略球的大小,可看作一点)以原来的速度向相反的方向运动:设运动的时间为(秒).
①分别表示甲、乙两小球到原点的距离(用t表示);
②求甲、乙两小球到原点的距离相等时经历的时间
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在矩形ABCD中,AB=2,BC=6,直线EF经过对角线BD的中点O,分别交边AD,BC于点E,F,点G,H分别是OB,OD的中点,当四边形EGFH为矩形时,则BF的长_________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
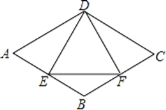
【题目】如图,在菱形ABCD中,E是AB边上一点,且∠A=∠EDF=60°,有下列结论:①AE=BF;②△DEF是等边三角形;③△BEF是等腰三角形;④∠ADE=∠BEF,其中结论正确的个数是( )
A.3
B.4
C.1
D.2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:甲乙两车分别从相距300千米的A、B两地同时出发相向而行,其中甲到达B地后立即返回,如图是它们离各自出发地的距离y(千米)与行驶时间x(小时)之间的函数图象.

(1)求甲车离出发地的距离y甲(千米)与行驶时间x(小时)之间的函数关系式,并写出自变量的取值范围;
(2)它们出发![]() 小时时,离各自出发地的距离相等,求乙车离出发地的距离y乙(千米)与行驶时间x(小时)之间的函数关系式,并写出自变量的取值范围;
小时时,离各自出发地的距离相等,求乙车离出发地的距离y乙(千米)与行驶时间x(小时)之间的函数关系式,并写出自变量的取值范围;
(3)在(2)的条件下,求它们在行驶的过程中相遇的时间.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com