练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，已知AD∥BC，EF∥AD，AG平分∠BAD，∠AGB=90°．请问BG平分∠ABC吗？说明理由．

    【答案】BG平分，理由见解析.

    【解析】

    先根据EF∥AD得出∠6=∠1，再根据∠AGB=90°可知∠5=90°﹣∠1，由平行线的传递性得出EF∥BC，故可得出∠3=∠5，由平行线的性质及等式的性质可得出∠4=90°﹣∠1，进而得出结论．

    BG平分∠ABC．理由如下：

    ∵EF∥AD，∴∠6=∠1．

    ∵∠AGB=90°，∴∠5=90°﹣∠6=90°﹣∠1．

    ∵AD∥BC，EF∥AD，∴EF∥BC，∴∠3=∠5．

    ∵AD∥BC，∠1=∠2，∴（∠3+∠4）+（∠2+∠1）=180°，即（90°﹣∠1+∠4）+2∠1=180°，∴∠4=90°﹣∠1，∴∠3=∠4，即BG平分∠ABC．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，矩形ABCD中，AB=4，BC=2，E是AB的中点，直线平行于直线EC，且直线与直线EC之间的距离为2，点F在矩形ABCD边上，将矩形ABCD沿直线EF折叠，使点A恰好落在直线上， 则DF的长为_____

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，抛物线与轴交于A、B两点（A点在B点左侧），与轴交于点C，连接BC、AC，tan∠OCB -tan∠OCA=1，OB=4OA.

    （1）求和b的值；

    （2）点E在线段BC上，点F在BC的延长线上，且BE=CF，点D是直线BC下方抛物线上一点，当△EDF是以EF为斜线的直角三角形，且4ED=3FD时，求D点坐标；

    （3）在（2）的条件下，过点A作AG⊥轴，R为抛物线上CD段上一点，连接AR，点K在AR上，连接DK并延长交AG于点G，连接DR，且2∠RDK+∠RKD=90°，∠GAR=∠RDK，若点M（）w为坐标平面内一点，直线MD与直线BC交于点N，当MN=DN时，求△MRD的面积.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某公司购买了一批A、B型芯片，其中A型芯片的单价比B型芯片的单价少9元，已知该公司用3120元购买A型芯片的条数与用4200元购买B型芯片的条数相等．

    （1）求该公司购买的A、B型花片的单价各是多少元？

    （2）若两种芯片共购买了200条，且购买的总费用不超过6300元，求A型芯片至少购买多少条？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

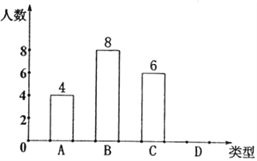
    【题目】某校260名学生参加献爱心捐款活动，每人捐款4～7元，活动结束后随机抽查了20名学生每人的捐款数量，并按每人的捐款数量分为四种类型，A：捐款4元；B：捐款5元；C：捐款6元；D：捐款7元，并将其绘成如图所示的条形统计图.

    （1）通过计算补全条形统计图；

    （2）直接写出这20名学生每人捐款数量的众数和中位数；

    （3）求这20名学生每人捐款数量的的平均数，并估计260名学生共捐款多少元.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，菱形ABCD的对角线AC和BD相交于点O，AB＝，OA＝a，OB＝b，且a，b满足：．

    （1）求菱形ABCD的面积；

    （2）求的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

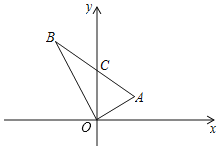
    【题目】如图，在平面直角坐标系中，O为原点，点A（2，1），B（﹣2，4），直线AB与y轴交于点C．

    （1）求点C的坐标；

    （2）求证：△OAB是直角三角形．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】现有正方形ABCD和一个以O为直角顶点的三角板，移动三角板，使三角板的两直角边所在直线分别与直线BC，CD交于点M，N．

    （1）如图1，若点O与点A重合，则OM与ON的数量关系是__________________；

    （2）如图2，若点O在正方形的中心（即两对角线的交点），则（1）中的结论是否仍然成立？请说明理由；

    （3）如图3，若点O在正方形的内部（含边界），当OM=ON时，请探究点O在移动过程中可形成什么图形？

    （4）如图4是点O在正方形外部的一种情况．当OM=ON时，请你就“点O的位置在各种情况下（含外部）移动所形成的图形”提出一个正确的结论．（不必说理）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某超市要销售一种新上市的文具，进价为20元，试营销阶段发现：当销售单价是25元时，每天的销售量为250件，销售单价每上涨1元，每天的销售量就减少10件．

    （1）求销售单价为多少元时，该文具每天的销售利润最大，并求出最大的利润；

    （2）经过试营销后，超市按（1）中单价销售，为了回馈广大顾客，同时提高该文具知名度，超市决定在1月1日当天开展降价促销活动，若每件文具降价2a%，则可多售出4a%，结果当天销售额为5670元，要使销量尽可能地大，求a的值．

    查看答案和解析>>

    同步练习册答案