
若正比例函数y1=﹣x的图象与一次函数y2=x+m的图象交于点A,且点A的横坐标为﹣1.
(1)求该一次函数的解析式;
(2)直接写出方程组
 的解;
的解;
(3)在一次函数y2=x+m的图象上求点B,使△AOB(O为坐标原点)的面积为2.
【考点】待定系数法求一次函数解析式.
【分析】(1)先将x=﹣1代入y=﹣x,求出y的值,得到点A坐标,再将点A坐标代入y=x+m,利用待定系数法可得一次函数的解析式;
(2)方程组的解就是正比例函数y=﹣x的图象与一次函数y=x+m的交点,根据交点坐标即可写出方程组的解;
(3)根据三角形的面积公式解答即可.
【解答】解:(1)将x=﹣1代入y=﹣x,得y=1,
则点A坐标为(﹣1,1).
将A(﹣1,1)代入y=x+m,得﹣1+m=1,
解得m=2,
所以一次函数的解析式为y=x+2;
(2)方程组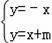
 的解为
的解为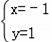
 ;
;
(3)设直线直线y=x+2与y轴的交点为C,与x轴的交点为D,则C(0,2),D(﹣2,0),
∵A(﹣1,1),
∴S△AOC=S△AOD=
 ×2×1=1,
×2×1=1,
①当B点在第一象限时,则S△BOC=1,
设B的横坐标为m,
∴S△BOC=
 ×2×m=1,解得m=1,
×2×m=1,解得m=1,
∴B(1,3);
②当B点在第三象限时,则S△BOD=1,
设B的纵坐标为n,
∴S△BOD=
 ×2×(﹣n)=1,解得n=﹣1,
×2×(﹣n)=1,解得n=﹣1,
∴B(﹣3,﹣1).
综上,B的坐标为(1,3)或(﹣3,﹣1).
【点评】本题考查了待定系数法求一次函数的解析式,方程组和函数的关系,三角形的面积等,分类讨论思想的运用是本题的关键.


科目:初中数学 来源: 题型:
如图,⊙O是以数轴原点O为圆心,半径为3的圆,与坐标轴的正半轴分别交于A、C两点,OB平分∠AOC,点P在数轴上运动,过点P且与OB平行的直线与⊙O有公共点,则线段OP的取值范围是 .


查看答案和解析>>
科目:初中数学 来源: 题型:
.有A,B两个黑布袋,A布袋中有两个完全相同的小球,分别标有数字1和2.B 布袋中有三个完全相同的小球,分别标有数字﹣1,﹣2和﹣3.小明从A布袋中随机取出一个小球,记录其标有的数字为x,再从B布袋中随机取出一个小球,记录其标有的数字为y,这样就确定点Q的一个坐标为(x,y).
(1)用列表或画树状图的方法写出点Q的所有可能坐标;
(2)求点Q落在直线y=﹣x﹣1上的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,Rt△ABC中,∠ACB=90°,∠A=50°,将其折叠,使点A落在边CB上A′处,折痕为CD,则∠A′DB=( )
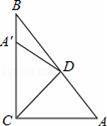

A.40° B.30° C.20° D.10°
查看答案和解析>>
科目:初中数学 来源: 题型:
设m是不小于﹣1的实数,关于x的方程x2+2(m﹣2)x+m2﹣3m+3=0有两个不相等的实数根x1、x2,
(1)若x12+x22=6,求m值;
(2)求
 的最大值.
的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
甲队修路150m与乙队修路120m所用天数相同,已知甲队比乙队每天多修10m,设甲队每天修路xm.依题意,下面所列方程正确的是( )
A.
 =
=
 B.
B.
 =
=
 C.
C.
 =
=
 D.
D.
 =
=

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com