
【题目】计算(1)![]()
(2)![]()
(3)![]()
【答案】(1)2m2﹣4mn﹣3n2;(2)6x2y;(3)18a6
【解析】
(1)根据完全平方公式和平方差公式进行计算,然后合并同类项,即可得到答案;
(2)先计算积的乘方,然后计算整式乘法和除法,即可得到答案;
(3)先计算乘方,然后计算同底数幂乘法,再合并同类项,即可得到答案.
解:(1)(2m+n)(2m﹣n)﹣2(m+n)2
=4m2﹣n2﹣2m2﹣4mn﹣2n2
=2m2﹣4mn﹣3n2.
(2)(﹣3x2y)2(6xy3)÷(9x3y4)
=9x4y26xy3÷9x3y4
=54x5y5÷9x3y4
=6x2y;
(3)(2a2)3+(﹣3a3)2+(a2)2a2
=23×(a2)3+(﹣3)2×(a3)2+(a2)2×a2
=8a6+9a6+a6
=(8+9+1)a6
=18a6.


 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案科目:初中数学 来源: 题型:
【题目】为了迎接“炎帝故里寻根节”,某校开展了主题为“炎帝文化知多少”的专题调查活动,采取随机抽样的方式进行问卷调查,问卷调查的结果分为“非常了解”“比较了解”“基本了解”“不太了解”四个等级,整理调查数据制成了下面的表格和如图所示的不完整的扇形统计图.
等级 | 非常了解 | 比较了解 | 基本了解 | 不太了解 |
频数 | 50 | m | 40 | 20 |

根据以上提供的信息,解答下列问题:
(1)本次问卷调查共抽取的学生人数为________,表中m的值为________;
(2)计算等级为“非常了解”的频数在扇形统计图中对应扇形的圆心角的度数,并补全扇形统计图;
(3)若该校有学生1 500人,请根据调查结果估计这些学生中“不太了解”炎帝文化知识的人数约为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数![]() (
(![]() 为常数)
为常数)
(1)该函数的图像与![]() 轴公共点的个数是( )
轴公共点的个数是( )
A.0 B.1 C.2 D.1或2
(2)求证:不论![]() 为何值,该函数的图像的顶点都在函数
为何值,该函数的图像的顶点都在函数![]() 的图像上.
的图像上.
(3)当![]() 时,求该函数的图像的顶点纵坐标的取值范围.
时,求该函数的图像的顶点纵坐标的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
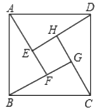
【题目】如图,将矩形ABCD的四个角向内折起,恰好拼成一个无缝隙无重叠的四边形EFGH,EH=12厘米,EF=16厘米,则边AD的长是( )

A. 12厘米 B. 16厘米 C. 20厘米 D. 28厘米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b(k、b为常数,k≠0)的图象与x轴、y轴分别交于A、B两点,且与反比例函数y=![]() (n为常数,且n≠0)的图象在第二象限交于点C.CD⊥x轴,垂足为D,若OB=2OA=3OD=12.
(n为常数,且n≠0)的图象在第二象限交于点C.CD⊥x轴,垂足为D,若OB=2OA=3OD=12.
(1)求一次函数与反比例函数的解析式;
(2)记两函数图象的另一个交点为E,求△CDE的面积;
(3)直接写出不等式kx+b≤![]() 的解集.
的解集.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一堤坝的坡角∠ABC=60°,坡面长度AB=24米(图为横截面).为了使堤坝更加牢固,需要改变堤坝的坡面,为使得坡面的坡角∠ADB=45°,则应将堤坝底端向外拓宽(BD)多少米?(结果精确到0.1米)(参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)
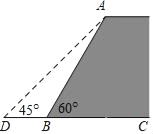
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年的暑假,李刚和他的父母计划去新疆旅游,他们打算坐飞机到乌鲁木齐,第二天租用一辆汽车自驾出游.

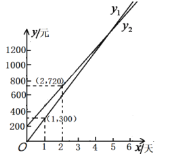
根据以上信息,解答下列问题:
(1)设租车时间为![]() 天,租用甲公司的车所需费用为
天,租用甲公司的车所需费用为![]() 元,租用乙公司的车所需费用为
元,租用乙公司的车所需费用为![]() 元,分别求出
元,分别求出![]() ,
,![]() 关于
关于![]() 的函数表达式;
的函数表达式;
(2)请你帮助李刚,选择租用哪个公司的车自驾出游比较合算,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于等腰三角形,以下说法正确的是( )
A.有一个角为40°的等腰三角形一定是锐角三角形
B.等腰三角形两边上的中线一定相等
C.两个等腰三角形中,若一腰以及该腰上的高对应相等,则这两个等腰三角形全等
D.等腰三角形两底角的平分线的交点到三边距离相等
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】赵爽(约公元182~250年),我国历史上著名的数学家与天文学家,他详细解释了《周髀算经》中勾股定理,将勾股定理表述为:“勾股各自乘,并之为弦实.开方除之,即弦.”又给出了新的证明方法“赵爽弦图”,巧妙地利用平面解析几何面积法证明了勾股定理.如图所示的“赵爽弦图”是由四个全等的直角三角形和中间一个小正方形拼成的一个大正方形,如果小正方形的面积为1,直角三角形较长直角边长为4,则大正方形的面积为_____________________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com