
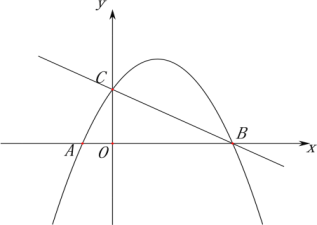
【题目】如图,已知A(-1,0),一次函数![]() 的图像交坐标轴于点B、C,二次函数
的图像交坐标轴于点B、C,二次函数![]() 的图像经过点A、C、B.点Q是二次函数图像上一动点。
的图像经过点A、C、B.点Q是二次函数图像上一动点。
(1)当![]() 时,求点Q的坐标;
时,求点Q的坐标;
(2)过点Q作直线![]() //BC,当直线
//BC,当直线![]() 与二次函数的图像有且只有一个公共点时,求出此时直线
与二次函数的图像有且只有一个公共点时,求出此时直线![]() 对应的一次函数的表达式并求出此时直线
对应的一次函数的表达式并求出此时直线![]() 与直线BC之间的距离。
与直线BC之间的距离。
【答案】(1)Q(0,2)或(3,2)或Q(![]() ,-2)或Q(
,-2)或Q(![]() ,-2);(2)一次函数
,-2);(2)一次函数![]() ,此时直线
,此时直线![]() 与直线BC之间的距离为
与直线BC之间的距离为![]()
【解析】
(1)根据![]() 可求得Q点的纵坐标,将Q点的纵坐标代入求得的二次函数解析式中求出Q点的横坐标,即可求得Q点的坐标;
可求得Q点的纵坐标,将Q点的纵坐标代入求得的二次函数解析式中求出Q点的横坐标,即可求得Q点的坐标;
(2)根据两直线平行可得直线l的一次项系数,因为直线与抛物线只有一个交点,所以联立它们所形成的方程组有两个相同的解可求得直线l的常数项,即可得到它的解析式.利用等面积法可求得原点距离两直线的距离,距离差即为直线![]() 与直线BC之间的距离.
与直线BC之间的距离.
解:(1)对于一次函数![]() ,
,
当x=0时,y=2,所以C(0,2),当y=0时,x=4,所以B(4,0).
∴![]() .
.
∴![]() 则
则![]() ,
,
将A、B带入二次函数解析式得![]() ,解得
,解得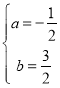 ,
,
∴二次函数解析式为:![]() ,
,
当y=2时,![]() ,解得
,解得![]() ,
,
所以![]() ,
,
当y=-2时,![]() ,解得
,解得![]() ,
,
所以![]() ,
,
故Q(0,2)或(3,2)或Q(![]() ,-2)或Q(
,-2)或Q(![]() ,-2).
,-2).
(2)根据题意设一次函数![]() ,
,
∵直线![]() 与二次函数的图像有且只有一个公共点
与二次函数的图像有且只有一个公共点
∴![]() 只有一个解,
只有一个解,
整理得![]() ,
,
∴![]() ,解得b=4,
,解得b=4,
∴一次函数![]()
如下图,直线l与坐标轴分别相交于D,E,过O作直线BC的垂线与BC和DE相交于F和G,
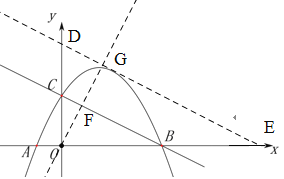
对于一次函数![]() ,当x=0时,y=4,故D(0,4),当y=0时,x=8,故E(8,0).
,当x=0时,y=4,故D(0,4),当y=0时,x=8,故E(8,0).
∴![]() ,
,
![]() ,即
,即![]() ,解得
,解得![]() ,
,
![]() ,即
,即![]() ,解得
,解得![]() ,
,
∴![]() .
.
∴此时直线![]() 与直线BC之间的距离为
与直线BC之间的距离为![]() .
.


 全优点练单元计划系列答案
全优点练单元计划系列答案科目:初中数学 来源: 题型:
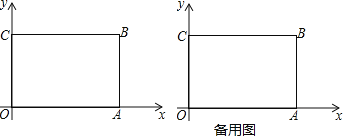
【题目】如图,矩形![]() 摆放在平面直角坐标系
摆放在平面直角坐标系![]() 中,点
中,点![]() 在
在![]() 轴上,点
轴上,点![]() 在
在![]() 轴上,
轴上,![]() .
.
(1)求直线![]() 的表达式;
的表达式;
(2)若直线![]() 与矩形
与矩形![]() 有公共点,求
有公共点,求![]() 的取值范围;
的取值范围;
(3)直线![]() 与矩形
与矩形![]() 没有公共点,直接写出
没有公共点,直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有两个全等的含30°角的直角三角板重叠在一起,如图,将△A′B′C′绕AC的中点M转动,斜边A′B′刚好过△ABC的直角顶点C,且与△ABC的斜边AB交于点N,连接AA′、C′C、AC′.若AC的长为2,有以下五个结论:①AA′=1;②C′C⊥A′B′;③点N是边AB的中点;④四边形AA′CC′为矩形;⑤A′N=B′C=![]() ,其中正确的有( )
,其中正确的有( )
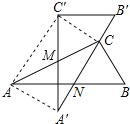
A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“校园读诗词诵经典比赛”结束后,评委刘老师将此次所有参赛选手的比赛成绩(得分均为整数)进行整理,并分别绘制成扇形统计图和频数直方图,部分信息如下图:
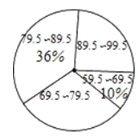
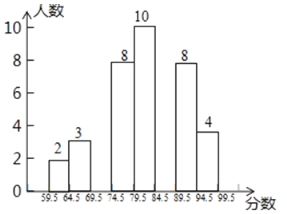
扇形统计图 频数直方图
(1)参加本次比赛的选手共有________人,参赛选手比赛成绩的中位数在__________分数段;补全频数直方图.
(2)若此次比赛的前五名成绩中有![]() 名男生和
名男生和![]() 名女生,如果从他们中任选
名女生,如果从他们中任选![]() 人作为获奖代表发言,请利用表格或画树状图求恰好选中
人作为获奖代表发言,请利用表格或画树状图求恰好选中![]() 男
男![]() 女的概率.
女的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是二次函数y=ax2+bx+c的图象,其对称轴为x=1,下列结论:①abc>0;②2a+b=0;③4a+2b+c<0;④若(-![]() ,y1),(
,y1),(![]() ,y2)是抛物线上两点,则y1<y2, 其中结论正确的是________.
,y2)是抛物线上两点,则y1<y2, 其中结论正确的是________.
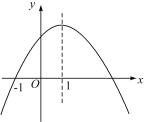
查看答案和解析>>
科目:初中数学 来源: 题型:
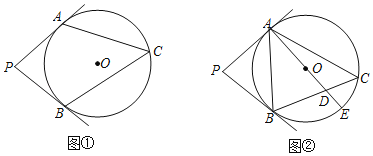
【题目】已知PA,PB分别与⊙O相切于点A,B,∠APB=80°,C为⊙O上一点.
(1)如图①,求∠ACB的大小;
(2)如图②,AE为⊙O的直径,AE与BC相交于点D.若AB=AD,求∠EAC的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,![]() 的三个顶点的坐标分别为点
的三个顶点的坐标分别为点![]() 、
、![]() 、
、![]() .
.
(1)![]() 的外接圆圆心
的外接圆圆心![]() 的坐标为 .
的坐标为 .
(2)①以点![]() 为位似中心,在网格区域内画出
为位似中心,在网格区域内画出![]() ,使得
,使得![]() 与
与![]() 位似,且点
位似,且点![]() 与点
与点![]() 对应,位似比为2:1,②点
对应,位似比为2:1,②点![]() 坐标为 .
坐标为 .
(3)![]() 的面积为 个平方单位.
的面积为 个平方单位.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com