
已知a,b,c是△ABC三条边的长,那么方程cx2+(a+b)x+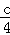 =0的根的情况是( )
=0的根的情况是( )
A.没有实数根 B.有两个不相等的正实数根
C.有两个不相等的负实数根 D.有两个异号实数根
C【考点】根与系数的关系;根的判别式;三角形三边关系.
【专题】压轴题.
【分析】判断上述方程的根的情况,只要看根的判别式△=b2﹣4ac的值的符号,结合三角形三边关系即可作出判断.
【解答】解:在此方程中△=b2﹣4ac=(a+b)2﹣4c×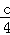 =(a+b)2﹣c2
=(a+b)2﹣c2
∵a,b,c是△ABC三条边的长
∴a>0,b>0,c>0.c<a+b,即(a+b)2>c2
∴△=(a+b)2﹣c2>0
故方程有两个不相等的实数根.
又∵两根的和是﹣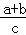 <0,两根的积是
<0,两根的积是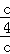 =
= >0
>0
∴方程有两个不等的负实根.
故选C
【点评】总结:一元二次方程根的情况与判别式△的关系:
(1)△>0⇔方程有两个不相等的实数根;
(2)△=0⇔方程有两个相等的实数根;
(3)△<0⇔方程没有实数根.
三角形三边关系:两边之和大于第三边,两边之差小于第三边.


科目:初中数学 来源: 题型:
两个大小不同的等腰直角三角形三角板如图1所示放置,图2是由它抽象出的几何图形,AB=AC,AE=AD,∠BAC=∠EAD=90°,
| |
(1)请找出图2中与△ABE全等的三角形,并给予证明( 说明:结论中不得含
说明:结论中不得含
有未标识的字母);
 (2)求证:DC⊥BE.
(2)求证:DC⊥BE.
查看答案和解析>>
科目:初中数学 来源: 题型:
已知关于x的方程x2﹣(2k+1)x+4(k﹣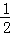 )=0,若等腰三角形ABC的一边长a=4,另一边长b、c恰好是这个方程的两个实数根,求△ABC的周长.
)=0,若等腰三角形ABC的一边长a=4,另一边长b、c恰好是这个方程的两个实数根,求△ABC的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
一只蜗牛从A点出发,在一条数轴上来回爬行,规定:向正半轴运动记为“+”,向负半轴运动记为“﹣”,从开始到结束爬行的各段路程(单位:cm)依次为+7,﹣5,﹣10,﹣8,+9,﹣6,+12,+4.
(1)若A点在数轴上表示的数为﹣2,则蜗牛停在数轴上何处,请通过计算加以说明.
(2)若蜗牛的爬行速度为每秒 cm,请问蜗牛一共爬行了多少秒?
cm,请问蜗牛一共爬行了多少秒?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com