
两个大小不同的等腰直角三角形三角板如图1所示放置,图2是由它抽象出的几何图形,AB=AC,AE=AD,∠BAC=∠EAD=90°,
| |
(1)请找出图2中与△ABE全等的三角形,并给予证明( 说明:结论中不得含
说明:结论中不得含
有未标识的字母);
 (2)求证:DC⊥BE.
(2)求证:DC⊥BE.
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案科目:初中数学 来源: 题型:
某航空公司有若干个飞机场,每两个飞机场之间都开辟一条航线,一共开辟了10条航线,则这个航空公司共有飞机场( )
A.4个 B.5个 C.6个 D .7个
.7个
查看答案和解析>>
科目:初中数学 来源: 题型:
已知a,b,c是△ABC三条边的长,那么方程cx2+(a+b)x+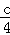 =0的根的情况是( )
=0的根的情况是( )
A.没有实数根 B.有两个不相等的正实数根
C.有两个不相等的负实数根 D.有两个异号实数根
查看答案和解析>>
科目:初中数学 来源: 题型:
方程(x﹣1)(x+3)=12化为ax2+bx+c=0的形式后,a、b、c的值为( )
A. 1、2、﹣15 B.1、﹣2、﹣15 C.﹣1、﹣2、﹣15 D.﹣1、2、﹣15
1、2、﹣15 B.1、﹣2、﹣15 C.﹣1、﹣2、﹣15 D.﹣1、2、﹣15
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com