练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

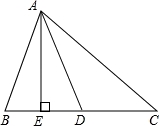
    如图，若AE是△ABC边上的高，∠EAC的角平分线AD交BC于D，∠ACB=40°，求∠ADE．

     


    【考点】三角形内角和定理；三角形的角平分线、中线和高．

    【分析】根据直角三角形两锐角互余求出∠CAE，再根据角平分线的定义可得∠DAE=∠CAE，进而得出∠ADE．

    【解答】解：∵AE是△ABC边上的高，∠ACB=40°，

    ∴∠CAE=90°﹣∠ACB=90°﹣40°=50°，

    ∴∠DAE=∠CAE=×50°=25°，

    ∴∠ADE=65°．

    【点评】本题考查了三角形的内角和定理，角平分线的定义，是基础题，熟记定理与概念并准确识图是解题的关键．

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    测量一段河水的深度，小丁把一根竹竿竖直插到离岸边1.5m远的水底，竹竿高出水面0.5m，把竹竿的顶端拉向岸边，竿顶和岸边的水面刚好相齐，则河水有多少深            (        )

    A．2.25m        B．2.5m         C．2m       D．3m

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    （a＋1）－2（a－2）．

     

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    到△ABC的三条边距离相等的点是△ABC的(     )

    A．三条中线交点 B．三条角平分线交点

    C．三条高的交点 D．三条边的垂直平分线交点

     

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，A，B两点的坐标分别是A（1，2），B（2，0），则△ABO的面积是__________．

     

    查看答案和解析>>

    科目：初中数学 来源： 题型：


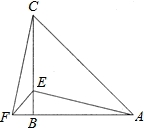
    在△ABC中，AB=CB，∠ABC=90°，F为AB延长线上一点，点E在BC上，且AE=CF．

    （1）求证：Rt△ABE≌Rt△CBF；

    （2）若∠CAE=30°，求∠ACF的度数．

     

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    六边形的内角和与外角和的度数分别是（      ）

    A．1080°,180° B．1080°,360°

     C．720°,180°  D．720°,360°

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    两个大小不同的等腰直角三角形三角板如图1所示放置，图2是由它抽象出的几何图形，AB=AC,AE=AD,∠BAC=∠EAD=90°，

     
    B、C、E在同一条直线上，连结DC．

    （1）请找出图2中与△ABE全等的三角形，并给予证明（说明：结论中不得含

    有未标识的字母）；

    （2）求证：DC⊥BE.

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    方程化为一元二次方程的一般形式是__________，它的一次项系数是__________．

    查看答案和解析>>

    同步练习册答案