
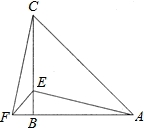
在△ABC中,AB=CB,∠ABC=90°,F为AB延长线上一点,点E在BC上,且AE=CF.
(1)求证:Rt△ABE≌Rt△CBF;
(2)若∠CAE=30°,求∠ACF的度数.
【考点】全等三角形的判定与性质.
【专题】几何图形问题;证明题;数形结合.
【分析】(1)由AB=CB,∠ABC=90°,AE=CF,即可利用HL证得Rt△ABE≌Rt△CBF;
(2)由AB=CB,∠ABC=90°,即可求得∠CAB与∠ACB的度数,即可得∠BAE的度数,又由Rt△ABE≌Rt△CBF,即可求得∠BCF的度数,则由∠ACF=∠BCF+∠ACB即可求得答案.
【解答】(1)证明:∵∠ABC=90°,
∴∠CBF=∠ABE=90°,
在Rt△ABE和Rt△CBF中,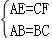 ,
,
∴Rt△ABE≌Rt△CBF(HL);
(2)解:∵AB=BC,∠ABC=90°,
∴∠CAB=∠ACB=45°,
又∵∠BAE=∠CAB﹣∠CAE=45°﹣30°=15°,
由(1)知:Rt△ABE≌Rt△CBF,
∴∠BCF=∠BAE=15°,
∴∠ACF=∠BCF+∠ACB=45°+15°=60°.
【点评】此题考查了直角三角形全等的判定与性质.此题难度不大,解题的关键是注意数形结合思想的应用.


科目:初中数学 来源: 题型:
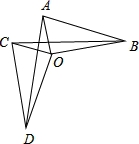
如图,OA=OC,OB=OD且OA⊥OB,OC⊥OD,下列结论:①△AOD≌△COB;②CD=AB;③∠CDA=∠ABC; 其中正确的结论是( )
A.①② B.①②③ C.①③ D.②③
查看答案和解析>>
科目:初中数学 来源: 题型:
等腰三角形的一个内角是50°,则另外两个角的度数分别是( )
A.65°,65° B.50°,80°
C. 50°,50° D. 65°,65°或50°,80°
查看答案和解析>>
科目:初中数学 来源: 题型:
某航空公司有若干个飞机场,每两个飞机场之间都开辟一条航线,一共开辟了10条航线,则这个航空公司共有飞机场( )
A.4个 B.5个 C.6个 D .7个
.7个
查看答案和解析>>
科目:初中数学 来源: 题型:
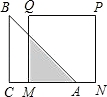
如图,已知等腰直角△ABC的直角边长与正方形MNPQ的边长均为20厘米,AC与MN在同一直线上,开始时点A与点N重合,让△ABC以每秒2厘米的速度向左运动,最终点A与点M重合,则重叠部分面积y(厘米2)与时间t(秒)之间的函数关系式为__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com