
如图,OA=OC,OB=OD且OA⊥OB,OC⊥OD,下列结论:①△AOD≌△COB;②CD=AB;③∠CDA=∠ABC; 其中正确的结论是( )
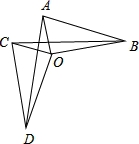
A.①② B.①②③ C.①③ D.②③
B【考点】全等三角形的判定与性质.
【分析】先由条件OA=OC,OB=OD且OA⊥OB,OC⊥OD就可以得出△COD≌△AOB,就有DD=BO,CD=AB,进而可以得出△AOD≌△COB就有∠ADO=∠CBO,从而得出结论.
【解答】解:∵OA⊥OB,OC⊥OD,
∴∠AOB=∠COD=90°.
∴∠AOB+∠AOC=∠COD+∠AOC,
即∠COB=∠AOD.
在△AOB和△COD中,
 ,
,
∴△AOB≌△COD(SAS),
∴AB=CD,∠ABO=∠CDO.
在△AOD和△COB中
 ,
,
∴△AOD≌△COB(SAS)
∴∠CBO=∠ADO,
∴∠ABO﹣∠CBO=∠CDO﹣∠ADO,
即∠ABC=∠CDA.
综上所述,①②③都是正确的.
故选B.
【点评】本题考查了全等三角形的判定与性质的运用,等式的性质的运用,解答时证明三角形全等是关键.


 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案科目:初中数学 来源: 题型:
如图, 一个4×2的矩形可以用3种不同的方式分割成2或5或8
个小正方形.
 |
⑴ 一个3×2的矩形用不同的方式分割后, 小正方形的个数可以是 ;
一个5×2的矩形用不同的方式分割后, 小正方形的个数可以是 ;
⑵ 一个n×2的矩形用不同的方式分割后,小正方形的个数最少是____________________.
(直接填写结果).
查看答案和解析>>
科目:初中数学 来源: 题型:
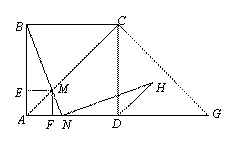
如图,在边长为2的正方形ABCD中,G是AD延长线上的一点,且DG=AD,动点M从A出发,以每秒1个单位的速度沿着A→C→G的路线向G点匀速运动(M不与A、G重合),设运动时间为t秒。连接BM并延长交AG于N。
(1)是否存在点M,使△ABM为等腰三角形?若存在,分析点M的位置;若不存在,请说明理由;
(2)当点N在AD边上时,若BN⊥H N,NH交∠CDG的平
N,NH交∠CDG的平 分线于H,求证:BN=NH;
分线于H,求证:BN=NH;
(3)过点M分别作AB、AD的垂线,垂足分别为E、F,矩形AEMF与△ACG重叠部分的面积为S,求S的最大值。
 |
查看答案和解析>>
科目:初中数学 来源: 题型:
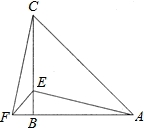
在△ABC中,AB=CB,∠ABC=90°,F为AB延长线上一点,点E在BC上,且AE=CF.
(1)求证:Rt△ABE≌Rt△CBF;
(2)若∠CAE=30°,求∠ACF的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com