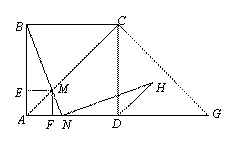
如图，在边长为2的正方形ABCD中，G是AD延长线上的一点，且DG=AD，动点M从A出发，以每秒1个单位的速度沿着A→C→G的路线向G点匀速运动（M不与A、G重合），设运动时间为t秒。连接BM并延长交AG于N。
（1）是否存在点M，使△ABM为等腰三角形？若存在，分析点M的位置；若不存在，请说明理由；
（2）当点N在AD边上时，若BN⊥H
N，NH交∠CDG的平分线于H，求证：BN=NH；
（3）过点M分别作AB、AD的垂线，垂足分别为E、F，矩形AEMF与△ACG重叠部分的面积为S，求S的最大值。
 |
科目：初中数学 来源： 题型：
如图，一副分别含有30°和45°角的两个直角三角板，拼成如下图形，其中∠C=90°，∠B=45°，∠E=30°，则∠BFD的度数是( )
A．15° B．25° C．30° D．10°
查看答案和解析>>
科目：初中数学 来源： 题型：
如图，OA=OC，OB=OD且OA⊥OB，OC⊥OD，下列结论：①△AOD≌△COB；②CD=AB；③∠CDA=∠ABC； 其中正确的结论是( )
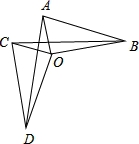
A．①② B．①②③ C．①③ D．②③
查看答案和解析>>
科目：初中数学 来源： 题型：
等腰三角形的一个内角是50°，则另外两个角的度数分别是（ ）
A．65°，65° B.50°，80°
C. 50°，50° D. 65°，65°或50°，80°
查看答案和解析>>
科目：初中数学 来源： 题型：
已知关于x的方程x2+（m+2）x+2m﹣1=0．
（1）求证：方程有两个不相等的实数根．
（2）当m为何值时，方程的两根互为相反数？并求出此时方程的解．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
，则代数式
的值为 ．
C．-2 D．-
，AD是∠BAC的平分线，若P、Q分别是AD和AC的动点，则PC+PQ的最小值是 ． 
的方程
。
：判断方程根的情况；
的值.