
已知关于x的方程x2+(m+2)x+2m﹣1=0.
(1)求证:方程有两个不相等的实数根.
(2)当m为何值时,方程的两根互为相反数?并求出此时方程的解.
【考点】根的判别式;根与系数的关系.
【专题】计算题.
【分析】(1)先计算出△=(m+2)2﹣4(2m﹣1),变形得到△=(m﹣2)2+4,由于(m﹣2)2≥0,则△>0,然后根据△的意义得到方程有两个不相等的实数根;
(2)利用根与系数的关系得到x1+x2=0,即m+2=0,解得m=﹣2,则原方程化为x2﹣5=0,然后利用直接开平方法求解.
【解答】(1)证明:△=(m+2)2﹣4(2m﹣1)
=m2﹣4m+8
=(m﹣2)2+4,
∵(m﹣2)2≥0,
∴(m﹣2)2+4>0,
即△>0,
所以方程有两个不相等的实数根;
(2)设方程的两个根为x1,x2,由题意得:
x1+x2=0,即m+2=0,解得m=﹣2,
当m=﹣2时,方程两根互为相反数,
当m=﹣2时,原方程为x2﹣5=0,
解得:x1=﹣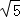 ,x2=
,x2=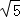 .
.
【点评】本题考查了一元二次方程ax2+bx+c=0(a≠0)的根的判别式△=b2﹣4ac:当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.也考查了解一元二次方程和根与系数的关系.


 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案科目:初中数学 来源: 题型:
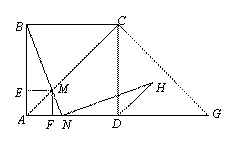
如图,在边长为2的正方形ABCD中,G是AD延长线上的一点,且DG=AD,动点M从A出发,以每秒1个单位的速度沿着A→C→G的路线向G点匀速运动(M不与A、G重合),设运动时间为t秒。连接BM并延长交AG于N。
(1)是否存在点M,使△ABM为等腰三角形?若存在,分析点M的位置;若不存在,请说明理由;
(2)当点N在AD边上时,若BN⊥H N,NH交∠CDG的平
N,NH交∠CDG的平 分线于H,求证:BN=NH;
分线于H,求证:BN=NH;
(3)过点M分别作AB、AD的垂线,垂足分别为E、F,矩形AEMF与△ACG重叠部分的面积为S,求S的最大值。
 |
查看答案和解析>>
科目:初中数学 来源: 题型:
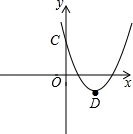
已知二次函数y=x2﹣2mx+m2﹣1(m≠0)的图象经过点(1,0).
(1)求二次函数的解析式;
(2)该抛物线与y轴交于点C,顶点为D,求C,D两点的坐标;
( 3)x轴上是否存在一点P,使得PC+PD最短?若P点存在,求出P点的坐标;若P点不存在,请说明理由.
3)x轴上是否存在一点P,使得PC+PD最短?若P点存在,求出P点的坐标;若P点不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
已知关于x的方程x2﹣(2k+1)x+4(k﹣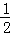 )=0,若等腰三角形ABC的一边长a=4,另一边长b、c恰好是这个方程的两个实数根,求△ABC的周长.
)=0,若等腰三角形ABC的一边长a=4,另一边长b、c恰好是这个方程的两个实数根,求△ABC的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
某土建工程共需动用15台挖运机械,每台机械每分钟能挖土3m3或者运土2m3.为了使挖土和运土工作同时结束,安排了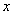 台机械运土,这里
台机械运土,这里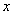 应满足的方程是( )
应满足的方程是( )
A.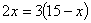 B.
B.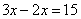 C.
C.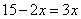 D.
D.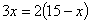
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com