
已知关于x的方程x2﹣(2k+1)x+4(k﹣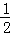 )=0,若等腰三角形ABC的一边长a=4,另一边长b、c恰好是这个方程的两个实数根,求△ABC的周长.
)=0,若等腰三角形ABC的一边长a=4,另一边长b、c恰好是这个方程的两个实数根,求△ABC的周长.
【考点】一元二次方程的应用;三角形三边关系;等腰三角形的性质.
【专题】计算题.
【分析】先利用因式分解法求出两根,再根据a=4为底边,a=4为腰,分别确定b,c的值,进而求出三角形的周长即可.
【解答】解:x2﹣(2k+1)x+4k﹣2=0,
整理得(x﹣2)[x﹣(2k﹣1)]=0,
∴x1=2,x2=2k﹣1,
当a=4为等腰△ABC的底边,则有b=c,
因为b、c恰是这个方程的两根,则2=2k﹣1,
解得k=1.5,
则三 角形的三边长分别为:2,2,4,
角形的三边长分别为:2,2,4,
∵2+2=4,这不满足三角形三边的关系,舍去;
当a=4为等腰△ABC的腰,
因为b、c恰是这个方程的两根,所以只能2k﹣1=4,
则三角形三边长分别为:2,4,4,
此时三角形的周长为2+4+4=10.
∴△ABC的周长为10.
【点评】考查一元二次方程的应用;分类探讨a=4是等腰三角形的一边的情况是解决本题的难点.


科目:初中数学 来源: 题型:
等腰三角形的一个内角是50°,则另外两个角的度数分别是( )
A.65°,65° B.50°,80°
C. 50°,50° D. 65°,65°或50°,80°
查看答案和解析>>
科目:初中数学 来源: 题型:
已知关于x的方程x2+(m+2)x+2m﹣1=0.
(1)求证:方程有两个不相等的实数根.
(2)当m为何值时,方程的两根互为相反数?并求出此时方程的解.
查看答案和解析>>
科目:初中数学 来源: 题型:
已知a,b,c是△ABC三条边的长,那么方程cx2+(a+b)x+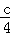 =0的根的情况是( )
=0的根的情况是( )
A.没有实数根 B.有两个不相等的正实数根
C.有两个不相等的负实数根 D.有两个异号实数根
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,已知等腰直角△ABC的直角边长与正方形MNPQ的边长均为20厘米,AC与MN在同一直线上,开始时点A与点N重合,让△ABC以每秒2厘米的速度向左运动,最终点A与点M重合,则重叠部分面积y(厘米2)与时间t(秒)之间的函数关系式为__________.
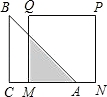
查看答案和解析>>
科目:初中数学 来源: 题型:
一种面粉的质量标识为“25±0.25千克”,则下列面粉中合格的( )
A.2 4.70千克 B.25.30千克 C.24.80千克 D.25.51千克
4.70千克 B.25.30千克 C.24.80千克 D.25.51千克
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com