
已知a,b,c是△ABC三条边的长,那么方程cx2+(a+b)x+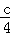 =0的根的情况是( )
=0的根的情况是( )
A.没有实数根 B.有两个不相等的正实数根
C.有两个不相等的负实数根 D.有两个异号实数根
C【考点】根与系数的关系;根的判别式;三角形三边关系.
【专题】压轴题.
【分析】判断上述方程的根的情况,只要看根的判别式△=b2﹣4ac的值的符号,结合三角形三边关系即可作出判断.
【解答】解:在此方程中△=b2﹣4ac=(a+b)2﹣4c×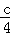 =(a+b)2﹣c2
=(a+b)2﹣c2
∵a,b,c是△ABC三条边的长
∴a>0,b>0,c>0.c<a+b,即(a+b)2>c2
∴△=(a+b)2﹣c2>0
故方程有两个不相等的实数根.
又∵两根的和是﹣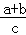 <0,两根的积是
<0,两根的积是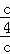 =
=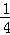 >0
>0
∴方程有两个不等的负实根.
故选C
【点评】总结:一元二次方程根的情况与判别式△的关系:
(1)△>0⇔方程有两个不相等的实数根;
(2)△=0⇔方程有两个相等的实数根;
(3)△<0⇔方程没有实数根.
三角形三边关系:两边之和大于第三边,两边之差小于第三边.


 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案科目:初中数学 来源: 题型:
已知二次函数y=x2﹣2mx+m2﹣1(m≠0)的图象经过点(1,0).
(1)求二次函数的解析式;
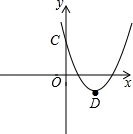
(2)该抛物线与y轴交于点C,顶点为D,求C,D两点的坐标;
( 3)x轴上是否存在一点P,使得PC+PD最短?若P点存在,求出P点的坐标;若P点不存在,请说明理由.
3)x轴上是否存在一点P,使得PC+PD最短?若P点存在,求出P点的坐标;若P点不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
已知关于x的方程x2﹣(2k+1)x+4(k﹣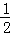 )=0,若等腰三角形ABC的一边长a=4,另一边长b、c恰好是这个方程的两个实数根,求△ABC的周长.
)=0,若等腰三角形ABC的一边长a=4,另一边长b、c恰好是这个方程的两个实数根,求△ABC的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
据统计,截止2014年1 2月28日,中国高铁运营总里程超过16000千米,稳居世界高铁里程榜首,将16000千米用科学记数法表示为1.6×10n米的形式,则n=__________.
2月28日,中国高铁运营总里程超过16000千米,稳居世界高铁里程榜首,将16000千米用科学记数法表示为1.6×10n米的形式,则n=__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com