
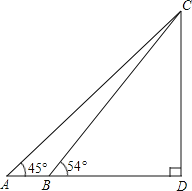
【题目】弦歌七十载,芬芳新时代,2019年9月21日郑州一中70年校庆之际,小明来到一中校园,参与到这隆重的庆典之中.在一中校园中参观之时,小明看到了一中秀丽的钟楼,想要测量钟楼的高度,如果钟楼的底部可以到达,如图,他在点A处测得钟楼最高点C的仰角为45°,再往钟楼方向前进至点B处测得最高点C的仰角为54°,AB=7m,根据测得的数据,计算钟楼的高度CD.(tan36°≈0.73,结果保留整数).
【答案】26m.
【解析】
首先根据题意得:∠CAD=45°,∠CBD=54°,AB=7m,在Rt△ACD中,易求得BD=AD-AB=CD-7;在Rt△BCD中,可得BD=CDtan36°,即可得CDtan36°=CD-7,继而求得答案.
根据题意得:∠CAD=45°,∠CBD=54°,AB=112m,
∵在Rt△ACD中,∠ACD=∠CAD=45°,
∴AD=CD,
∵AD=AB+BD,
∴BD=AD-AB=CD-7(m),
∵在Rt△BCD中,tan∠BCD=![]() ,∠BCD=90°-∠CBD=36°,
,∠BCD=90°-∠CBD=36°,
∴tan36°=![]() ,
,
∴BD=CDtan36°,
∴CDtan36°=CD-7,
∴CD=![]() ≈
≈![]() ≈26(m).
≈26(m).
答:钟楼的高度CD约为:26m.


科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx﹣3a经过点A(﹣1,0)、C(0,3),与x轴交于另一点B,抛物线的顶点为D.

(1)求此二次函数解析式;
(2)连接DC、BC、DB,求证:△BCD是直角三角形;
(3)在对称轴右侧的抛物线上是否存在点P,使得△PDC为等腰三角形?若存在,求出符合条件的点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
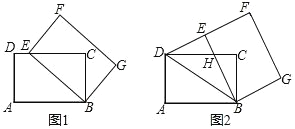
【题目】如图,在矩形 ABCD 中,AB=5,AD=3.以点 B 为中心,顺时针旋转矩形 BADC,得到矩形 BEFG,点 A、D、C 的对应点分别为 E、F、G.
(1)如图1,当点 E 落在 CD 边上时,求线段 CE 的长;
(2)如图2,当点 E 落在线段 DF 上时,求证:∠ABD=∠EBD;
(3)在(2)的条件下,CD 与 BE 交于点 H,求线段 DH 的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx﹣4a经过A(﹣1,0)、C(0,4)两点,与x轴交于另一点B,
(1)求抛物线的解析式;
(2)已知点D(m,m+1)在第一象限的抛物线上,求点D的坐标.
(3)设直线BC为y=mx+n(k≠0),若mx+n≥ax2+bx﹣4a,结合函数图象,写出x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从三角形(不是等腰三角形)一个顶点引出一条射线于对边相交,顶点与交点之间的线段把这个三角形分割成两个小三角形,如果分得的两个小三角形中一个为等腰三角形,另一个与原三角形相似,我们把这条线段叫做这个三角形的完美分割线.
(1)如图1,在△ABC中,CD为角平分线,∠A=40°,∠B=60°,求证:CD为△ABC的完美分割线.
(2)在△ABC中,∠A=48°,CD是△ABC的完美分割线,且△ACD为等腰三角形,求∠ACB的度数.
(3)如图2,△ABC中,AC=2,BC=![]() ,CD是△ABC的完美分割线,且△ACD是以CD为底边的等腰三角形,求完美分割线CD的长.
,CD是△ABC的完美分割线,且△ACD是以CD为底边的等腰三角形,求完美分割线CD的长.
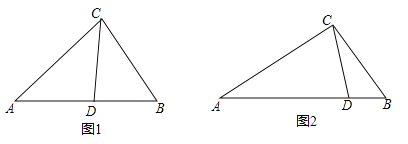
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有两个一元二次方程:M:![]() N:
N:![]() ,其中
,其中![]() ,以下列四个结论中,错误的是( )
,以下列四个结论中,错误的是( )
A、如果方程M有两个不相等的实数根,那么方程N也有两个不相等的实数根;
B、如果方程M有两根符号相同,那么方程N的两根符号也相同;
C、如果5是方程M的一个根,那么![]() 是方程N的一个根;
是方程N的一个根;
D、如果方程M和方程N有一个相同的根,那么这个根必是![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,其对称轴为直线x=﹣1,与x轴的交点为(x1,0)、(x2,0),其中0<x1<1,有下列结论:①abc>0;②﹣3<x2<﹣2;③4a﹣2b+c<﹣1;④当m为任意实数时,a﹣b<am2+bm;⑤若点(﹣0.5,y1),(﹣2,y2)均在抛物线上,则y1>y2;⑥a>![]() .其中,正确结论的个数为( )
.其中,正确结论的个数为( )
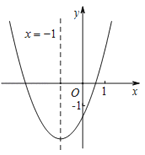
A.2B.3C.4D.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出以下结论:①b2>4ac;②abc>0;③2a﹣b=0;④8a+c<0;⑤9a+3b+c<0,其中结论正确的是 .(填正确结论的序号)
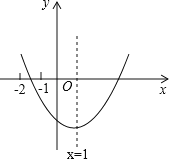
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB和抛物线的交点是A(0,-3),B(5,9),已知抛物线的顶点D的横坐标是2.

(1)求抛物线的解析式及顶点坐标;
(2)在![]() 轴上是否存在一点C,与A,B组成等腰三角形?若存在,求出点C的坐标,若不存在,请说明理由;
轴上是否存在一点C,与A,B组成等腰三角形?若存在,求出点C的坐标,若不存在,请说明理由;
(3)在直线AB的下方抛物线上找一点P,连接PA,PB使得△PAB的面积最大,并求出这个最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com