
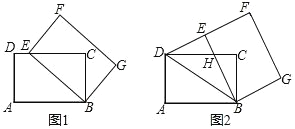
【题目】如图,在矩形 ABCD 中,AB=5,AD=3.以点 B 为中心,顺时针旋转矩形 BADC,得到矩形 BEFG,点 A、D、C 的对应点分别为 E、F、G.
(1)如图1,当点 E 落在 CD 边上时,求线段 CE 的长;
(2)如图2,当点 E 落在线段 DF 上时,求证:∠ABD=∠EBD;
(3)在(2)的条件下,CD 与 BE 交于点 H,求线段 DH 的长.
【答案】(1)4;(2)见解析;(3)DH= ![]() .
.
【解析】
(1)由旋转性质知BA=BE=5,由矩形性质知BC=AD=3,再在Rt△BCE中根据勾股定理可得;
(2)由旋转性质知∠BEF=∠A=90°,BE=BA,结合点E落在线段DF得∠BED=∠A=90°,再利用“HL”证△ABD≌△EBD即可得;
(3)设DH=x,从而得CH=5﹣x,再由矩形的性质知∠ABD=∠CDB,结合∠ABD=∠EBD知∠CDB=∠EBD,从而得DH=BH=x.在Rt△BCH中,根据CH2+BC2=BH2求解可得.
(1)由旋转的性质知BA=BE=5.
∵四边形ABCD是矩形,∴AD=BC=3,∠C=90°,∴CE![]() 4;
4;
(2)由旋转的性质知∠BEF=∠A=90°,BE=BA.
∵点E落在线段DF,∴∠BED=∠A=90°.
在△ABD和△EBD中,∵![]() ,∴△ABD≌△EBD(HL),∴∠ABD=∠EBD;
,∴△ABD≌△EBD(HL),∴∠ABD=∠EBD;
(3)设DH=x.
∵四边形ABCD是矩形,∴AB∥CD,AB=CD=5,∴CH=CD﹣DH=5﹣x,∠ABD=∠CDB.
又∵∠ABD=∠EBD,∴∠CDB=∠EBD,∴DH=BH=x.在Rt△BCH中,∵CH2+BC2=BH2,∴(5﹣x)2+32=x2,解得:x![]() ,∴DH
,∴DH![]() .
.


科目:初中数学 来源: 题型:
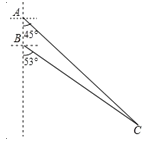
【题目】如图所示,我国两艘海监船 A,B 在南海海域巡逻,某一时刻,两船同时收到指令,立即前往救援遇险抛锚的渔船 C,此时,B 船在A 船的正南方向 15 海里处,A 船测得渔船 C 在其南偏东 45°方向,B 船测得渔船 C 在其南偏东 53°方向,已知 A 船的航速为 30 海里/小时,B 船的航速为 25 海里/小时,问 C 船至少要等待多长时间才能得到救援?(参考数据:sin53°≈![]() ,cos53°≈
,cos53°≈![]() ,tan53°≈ 4 ,
,tan53°≈ 4 ,![]() 1.41 )
1.41 )
查看答案和解析>>
科目:初中数学 来源: 题型:
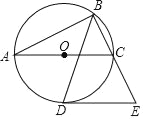
【题目】如图,以△ABC的边AC为直径的⊙O恰为△ABC的外接圆,∠ABC的平分线交⊙O于点D,过点D作DE∥AC交BC的延长线于点E.
(1)求证: DE是⊙O的切线;
(2)若AB=2![]() ,BC=
,BC=![]() ,求DE的长.
,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着我国经济社会的发展,人民对于美好生活的追求越来越高,外出旅游已成为时尚.某社区为了了解家庭旅游消费情况,随机抽取部分家庭,对每户家庭的年旅游消费金额进行问卷调査,根据调查结果绘制成两幅不完整的统计图表.请你根据统计图表提供的信息,解答下列问题:
组别 | 家庭年旅游消费金额x(元) | 户数 |
A | x≤4000 | 27 |
B | 4000< x≤8000 | a |
C | 8000< x≤12000 | 24 |
D | 12000< x≤16000 | 14 |
E | x>16000 | 6 |
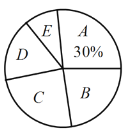
(1)本次被调査的家庭有 户,表中 a= ;
(2)本次调查数据的中位数出现在 组.扇形统计图中,E组所在扇形的圆心角是 度;
(3)若这个社区有2700户家庭,请你估计家庭年旅游消费8000元以上的家庭有多少户?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某批发商以每件50元的价格购进400件T恤.若以单价70元销售,预计可售出200件.批发商的销售策略是:第一个月为增加销售量,降价销售,经过市场调查,单价每降低0.5元,可多售出5件,但最低单价不低于购进的价格;第一个月结束后,将剩余的T恤一次性清仓销售,清仓时单价为40元.设第一个月单价降低x元.
(1)根据题意,完成下表:
每件T恤的利润(元) | 销售量(件) | |
第一个月 | ||
清仓时 |
(2)T恤的销售单价定为多少元时,该批发商可获得最大利润?最大利润为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
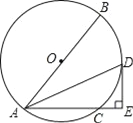
【题目】如图,已知⊙O的直径AB=10,弦AC=6,∠BAC的平分线交⊙O于点D,过点D作DE⊥AC交AC的延长线于点E.
(1)求证:DE是⊙O的切线.
(2)求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知矩形ABCD的一条边AD=8,E是BC边上的一点,将矩形ABCD沿折痕AE折叠,使得顶点B落在CD边上的点P处,PC=4(如图1).
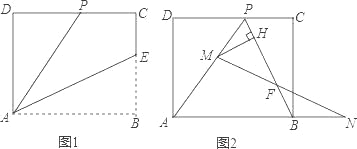
(1)求AB的长;
(2)擦去折痕AE,连结PB,设M是线段PA的一个动点(点M与点P、A不重合).N是AB沿长线上的一个动点,并且满足PM=BN.过点M作MH⊥PB,垂足为H,连结MN交PB于点F(如图2).
①若M是PA的中点,求MH的长;
②试问当点M、N在移动过程中,线段FH的长度是否发生变化?若变化,说明理由;若不变,求出线段FH的长度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com