
【题目】如图,在平面直角坐标系中,已知矩形OABC的两个顶点A、B的坐标分别![]()

(1)求对角线AC所在的直线的函数表达式;
(2)把矩形OABC以AC所在的直线为对称轴翻折,点O落在平面上的点D处,求点D的坐标;
(3)在平面内是否存在点P,使得以A、O、D、P为顶点的四边形为平行四边形?若存在,求出点P的坐标;若不存在,请说明理由。
【答案】(1)y=![]() x+2.
x+2.
(2)(-![]() ,3).
,3).
(3)(![]() ,3)或(-
,3)或(-![]() ,-3)或(-3
,-3)或(-3![]() ,3).
,3).
【解析】
(1)求出点C的坐标,利用待定系数法即可求出直线AC的函数表达式;
(2)过点D作DE⊥OA于点E,利用三角函数的知识,求出DE及OE的长度,即可得出点D的坐标.
(3)找到点P的可能位置,利用平行四边形对边相等的性质即可得出点P的坐标.
解:(1)由题意得,OA=2![]() ,∠CAO=30°,
,∠CAO=30°,
则OC=OAtan∠CAO=2,
即点C的坐标为(0,2),
设直线AC的解析式为:y=kx+b,将点A及点C的坐标代入得: ,
,
解得: ,
,
故直线AC的函数表达式为:y=![]() x+2.
x+2.
(2)过点D作DE⊥OA于点E,
∵∠CAO=30°,
∴∠DAE=60°,
又∵AD=AO=2![]() ,
,
∴DE=3,AE=![]() ,
,
∴OE=![]() ,
,
故点D的坐标为(-![]() ,3).
,3).
(3)
①当AD为平行四边形的一边时,点P的位置有两个,分别为P1、P2,
当点P位于P1位置时,DP1=AO,
此时可得点P的坐标为(![]() ,3);
,3);
当点P位于P2位置时,
∵OD=AD,△AOD是等边三角形,
∴点P2与点D关于x轴对称,
此时可得点P的坐标为(-![]() ,-3);
,-3);
②当AD为平行四边形的对角线时,点P的位置有一个,在P3的位置,
此时DP3=AO,
故可得点P的坐标为(-3![]() ,3).
,3).
综上可得存在点P的坐标,使得以A、O、D、P为顶点的四边形为平行四边形,点P的坐标为(![]() ,3)或(-
,3)或(-![]() ,-3)或(-3
,-3)或(-3![]() ,3).
,3).


科目:初中数学 来源: 题型:
【题目】如图:O是直线AB上一点,∠AOC=50°,OD是∠BOC的角平分线,OE⊥OC于点O.求∠DOE的度数.(请补全下面的解题过程)

解:∵O是直线AB上一点,∠AOC=50°,
∴∠BOC=180°-∠AOC= °.
∵ OD是∠BOC的角平分线,
∴∠COD= ∠BOC .( )
∴∠COD=65°.
∵OE⊥OC于点O,(已知).
∴∠COE= °.( )
∴∠DOE=∠COE-∠COD= ° .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将一段标有0~60均匀刻度的绳子铺平后折叠(绳子无弹性),使绳子自身的一部分重叠,然后在重叠部分沿绳子垂直方向剪断,将绳子分为A、B、C三段,若这三段的长度由短到长的比为1:2:3,则折痕对应的刻度不可能是( )
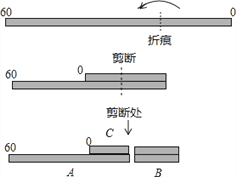
A. 20 B. 25 C. 30 D. 35
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列两个等式:2×![]() =22﹣2×
=22﹣2×![]() ﹣2,4×
﹣2,4×![]() =42﹣2×
=42﹣2×![]() ﹣2,给出定义如下:我们称使等式ab=a2﹣2b﹣2成立的一对有理数a,b为“方差有理数对”,记为(a,b),如:(2,
﹣2,给出定义如下:我们称使等式ab=a2﹣2b﹣2成立的一对有理数a,b为“方差有理数对”,记为(a,b),如:(2,![]() ),(4,
),(4,![]() )都是“方差有理数对”.
)都是“方差有理数对”.
(1)判断数对(﹣1,﹣1)是否为“方差有理数对”,并说明理由;
(2)若(m,2)是“方差有理数对”,求﹣6m﹣3[m2﹣2(2m﹣1)]的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在求两位数的平方时,可以用“列竖式”的方法进行速算,求解过程如图1所示.仿照图1,用“列竖式”的方法计算一个两位数的平方,部分过程如图2所示,若这个两位数的个位数字为a,则这个两位数为( )
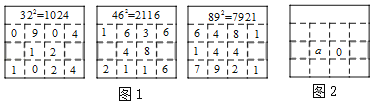
A.a﹣50B.a+50C.a﹣20D.a+20
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB与CD相交于点O,∠AOE=90°.

(1)如图1,若OC平分∠AOE,求∠AOD的度数;
(2)如图2,若∠BOC=4∠FOB,且OE平分∠FOC,求∠EOF的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,O为直线AB上一点,过点O作射线OC,∠AOC=30°,将一直角三角板(其中∠P=30°)的直角顶点放在点O处,一边OQ在射线OA上,另一边OP与OC都在直线AB的上方.将图1中的三角板绕点O以每秒3°的速度沿顺时针方向旋转一周.
(1)如图2,经过t秒后,OP恰好平分∠BOC.
①求t的值;
②此时OQ是否平分∠AOC?请说明理由;
(2)若在三角板转动的同时,射线OC也绕O点以每秒6°的速度沿顺时针方向旋转一周,如图3,那么经过多长时间OC平分∠POQ?请说明理由;
(3)在(2)问的基础上,经过多少秒OC平分∠POB?(直接写出结果).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若 x 满足 (9x)(x4)=4, 求 (4x)2+(x9)2 的值.
设 9x=a,x4=b, 则 (9x)(x4)=ab=4,a+b=(9x)+(x4)=5 ,
∴(9x)2+(x4)2=a2+b2=(a+b)22ab=522×4=13
请仿照上面的方法求解下面问题:
(1)若 x 满足 (5x)(x2)=2, 求 (5x)2+(x2)2 的值
(2)已知正方形 ABCD 的边长为 x , E , F 分别是 AD 、 DC 上的点,且 AE=1 , CF=3 ,长方形 EMFD 的面积是 48 ,分别以 MF 、 DF 作正方形,求阴影部分的面积.
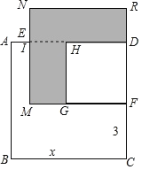
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx﹣3(a≠0)的顶点为E,该抛物线与x轴交于A、B两点,与y轴交于点C,且BO=OC,AO=DO,直线y=mx+1与y轴交于点D.
(1)求抛物线和直线的解析式;
(2)证明:△DBO∽△EBC;
(3)在抛物线的对称轴上是否存在点P,使△PBC是等腰三角形?若存在,请直接写出符合条件的P点坐标,若不存在,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com