
【题目】如图1,O为直线AB上一点,过点O作射线OC,∠AOC=30°,将一直角三角板(其中∠P=30°)的直角顶点放在点O处,一边OQ在射线OA上,另一边OP与OC都在直线AB的上方.将图1中的三角板绕点O以每秒3°的速度沿顺时针方向旋转一周.
(1)如图2,经过t秒后,OP恰好平分∠BOC.
①求t的值;
②此时OQ是否平分∠AOC?请说明理由;
(2)若在三角板转动的同时,射线OC也绕O点以每秒6°的速度沿顺时针方向旋转一周,如图3,那么经过多长时间OC平分∠POQ?请说明理由;
(3)在(2)问的基础上,经过多少秒OC平分∠POB?(直接写出结果).

【答案】(1)①5;②OQ平分∠AOC,理由详见解析;(2)5秒或65秒时OC平分∠POQ;(3)t=![]() 秒.
秒.
【解析】
(1)①由∠AOC=30°得到∠BOC=150°,借助角平分线定义求出∠POC度数,根据角的和差关系求出∠COQ度数,再算出旋转角∠AOQ度数,最后除以旋转速度3即可求出t值;②根据∠AOQ和∠COQ度数比较判断即可;
(2)根据旋转的速度和起始位置,可知∠AOQ=3t,∠AOC=30°+6t,根据角平分线定义可知∠COQ=45°,利用∠AOQ、∠AOC、∠COQ角之间的关系构造方程求出时间t;
(3)先证明∠AOQ与∠POB互余,从而用t表示出∠POB=90°﹣3t,根据角平分线定义再用t表示∠BOC度数;同时旋转后∠AOC=30°+6t,则根据互补关系表示出∠BOC度数,同理再把∠BOC度数用新的式子表达出来.先后两个关于∠BOC的式子相等,构造方程求解.
(1)①∵∠AOC=30°,
∴∠BOC=180°﹣30°=150°,
∵OP平分∠BOC,
∴∠COP=![]() ∠BOC=75°,
∠BOC=75°,
∴∠COQ=90°﹣75°=15°,
∴∠AOQ=∠AOC﹣∠COQ=30°﹣15°=15°,
t=15÷3=5;
②是,理由如下:
∵∠COQ=15°,∠AOQ=15°,
∴OQ平分∠AOC;
(2)∵OC平分∠POQ,
∴∠COQ=![]() ∠POQ=45°.
∠POQ=45°.
设∠AOQ=3t,∠AOC=30°+6t,
由∠AOC﹣∠AOQ=45°,可得30+6t﹣3t=45,
解得:t=5,
当30+6t﹣3t=225,也符合条件,
解得:t=65,
∴5秒或65秒时,OC平分∠POQ;
(3)设经过t秒后OC平分∠POB,
∵OC平分∠POB,
∴∠BOC=![]() ∠BOP,
∠BOP,
∵∠AOQ+∠BOP=90°,
∴∠BOP=90°﹣3t,
又∠BOC=180°﹣∠AOC=180°﹣30°﹣6t,
∴180﹣30﹣6t=![]() (90﹣3t),
(90﹣3t),
解得t=![]() .
.


 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案科目:初中数学 来源: 题型:
【题目】正方形A1B1C1O、A2B2C2C1、A3B3C3C2、……按如图的方式放置,点A1、A2、A3……和点C1、C2、C3……分别在直线y=x+1和x轴上,则点B6的坐标是( )
A. (31,16) B. (63,32) C. (15,8) D. (31,32)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电信公司有甲、乙两种手机收费业务,仅上网流量收费不同,图中I1、I2分别表示甲、乙两种业务每月流量费用y(元)与上网流量xGB的之间的函数关系。

(1)分别求出甲、乙两种业务每月所收费用y元与上网流量xGB之间的函数关系式。
(2)已知刘老师选择了甲业务,魏老师选择了乙业务,上月两位老师所用流量相同,均为mGB,上网流量费用相差不到20元,求m的取值范围。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知矩形OABC的两个顶点A、B的坐标分别![]()

(1)求对角线AC所在的直线的函数表达式;
(2)把矩形OABC以AC所在的直线为对称轴翻折,点O落在平面上的点D处,求点D的坐标;
(3)在平面内是否存在点P,使得以A、O、D、P为顶点的四边形为平行四边形?若存在,求出点P的坐标;若不存在,请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列条件中,能判定四边形ABCD为平行四边形的个数是( )
①AB∥CD,AD=BC ; ②AB=CD,AD=BC;③∠A=∠B,∠C=∠D; ④AB=AD,CB=CD.
A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
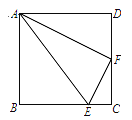
【题目】如图,在四边形ABCD中,AB=BC=CD=AD=4,∠DAB=∠B=∠C=∠D=90°,E,F分别是边BC,CD上的点,且CE=![]() BC,F为CD的中点,问△AEF是什么三角形?请说明理由.
BC,F为CD的中点,问△AEF是什么三角形?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察算式:1×3+1=4=22;2×4+1=9=32;3×5+1=16=42;4×6+1=25=52,…
(1)请根据你发现的规律填空:6×8+1=( )2;
(2)用含n的等式表示上面的规律: ;
(3)用找到的规律解决下面的问题:
计算:(1+![]() )(1+
)(1+![]() )(1+
)(1+![]() )(1+
)(1+![]() )…(1+
)…(1+![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
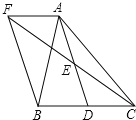
【题目】如图,在![]() 中,D是BC边上的一点,E是AD的中点,过A点作BC的平行线交CE的延长线于点F,且
中,D是BC边上的一点,E是AD的中点,过A点作BC的平行线交CE的延长线于点F,且![]() ,连接BF.
,连接BF.
![]() 证明:
证明:![]() ;
;
![]() 当
当![]() 满足什么条件时,四边形AFBD是矩形?并说明理由.
满足什么条件时,四边形AFBD是矩形?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《中国汉字听写大会》唤醒了很多人对文字基本功的重视和对汉字文化的学习,我市某校组织了一次全校2000名学生参加的“汉字听写大会”海选比赛,赛后发现所有参赛学生的成绩均不低于50分,为了更好地了解本次海选比赛的成绩分布情况,随机抽取了其中200名学生的海选比赛成绩(成绩x取整数,总分100分)作为样本进行整理,得到下列统计图表:

请根据所给信息,解答下列问题:
(1)请把图1中的条形统计图补充完整;
(2)在图2的扇形统计图中,记表示B组人数所占的百分比为a%,则a的值为 ,表示C组扇形的圆心角θ的度数为 度;
(3)规定海选成绩在90分以上(包括90分)记为“优等”,请估计该校参加这次海选比赛的2000名学生中成绩“优等”的有多少人?
(4)经过统计发现,在E组中,有2位男生和2位女生获得了满分,如果从这4人中挑选2人代表学校参加比赛,请用树状图或列表法求出所选两人正好是一男一女的概率是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com