
ЁОЬтФПЁПФГЕчаХЙЋЫОгаМзЁЂввСНжжЪжЛњЪеЗбвЕЮёЃЌНіЩЯЭјСїСПЪеЗбВЛЭЌЃЌЭМжаI1ЁЂI2ЗжБ№БэЪОМзЁЂввСНжжвЕЮёУПдТСїСПЗбгУyЃЈдЊЃЉгыЩЯЭјСїСПxGBЕФжЎМфЕФКЏЪ§ЙиЯЕЁЃ

ЃЈ1ЃЉЗжБ№ЧѓГіМзЁЂввСНжжвЕЮёУПдТЫљЪеЗбгУyдЊгыЩЯЭјСїСПxGBжЎМфЕФКЏЪ§ЙиЯЕЪНЁЃ
ЃЈ2ЃЉвбжЊСѕРЯЪІбЁдёСЫМзвЕЮёЃЌЮКРЯЪІбЁдёСЫвввЕЮёЃЌЩЯдТСНЮЛРЯЪІЫљгУСїСПЯрЭЌЃЌОљЮЊmGBЃЌЩЯЭјСїСПЗбгУЯрВюВЛЕН20дЊЃЌЧѓmЕФШЁжЕЗЖЮЇЁЃ
ЁОД№АИЁПЃЈ1ЃЉI1ЃКy=100xЃЛ
I2ЃК![]() ЃЛ
ЃЛ
ЃЈ2ЃЉ0.3ЃМmЃМ0.7ЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнЭМЯѓжаЬсЙЉЕФаХЯЂРћгУД§ЖЈЯЕЪ§ЗЈМДПЩЕУЕННсТлЃЛ
ЃЈ2ЃЉИљОнЬтвтМДПЩЕУЕННсТлЃЎ
НтЃКЃЈ1ЃЉЩшl1ЕФНтЮіЪНЮЊy=kxдђвРЬтвтЕУЃК
0.8k=80,НтЕУk=100.
Ёрl1ЕФНтЮіЪНЮЊy=100xЃЛ
гЩЭМЯѓПЩжЊЕБ0<x<1ЪБЃЌl2=50ЃЌЕБxЁн1ЪБЃЌЩшl2ЕФНтЮіЪНЮЊy=kx+bЃЌдђвРЬтвтЕУЃК
![]()
НтЕУЃК![]()
ЁрЕБxЁн1ЪБЃЌl2ЕФНтЮіЪНЮЊy=100x-50.
ЁрI1ЃКy=100xЃЛ
I2ЃК![]() ЃЛ
ЃЛ
ЃЈ2ЃЉгЩЭМЯѓжЊЃЌЕБxЃО1ЪБЃЌСНШЫЫљНЛЗбгУВюЯрЕШЃЌЧвВюЮЊ50ЃЌЫљвдЗбгУВюаЁгк20ЃЌдђxЃМ1ЃЌЙЪy1-y2ВюЕФОјЖджЕаЁгк20ЃЌЕУ0.3ЃМmЃМ0.7
ЁрmЕФШЁжЕЗЖЮЇЪЧЃК0.3ЃМmЃМ0.7ЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПздЪЕЪЉаТНЬг§ИФИяКѓЃЌбЇЩњЕФзджїбЇЯАЁЂКЯзїНЛСїФмСІгаКмДѓЬсИпЃЌеХРЯЪІЮЊСЫСЫНтЫљНЬАрМЖбЇЩњзджїбЇЯАЁЂКЯзїНЛСїЕФОпЬхЧщПіЃЌЖдБОАрВПЗжЭЌбЇНјааСЫЮЊЦкАыИідТЕФИњзйЕїВщЃЌВЂНЋЕїВщНсЙћЗжЮЊЫФРрЃКAЃЎЬиБ№КУЃЛBЃЎКУЃЛCЃЎвЛАуЃЛDЃЎНЯВюЃЌВЂНЋЕїВщНсЙћЛцжЦГЩвдЯТСНЗљВЛЭъећЕФЭГМЦЭМЃЌЧыФуИљОнЭГМЦЭМНтД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉБОДЮЕїВщжаЃЌеХРЯЪІвЛЙВЕїВщСЫЖрЩйУћЭЌбЇЃП
ЃЈ2ЃЉЧѓГіЕїВщжаCРрХЎЩњМАDРрФаЩњЕФШЫЪ§ЃЌНЋЬѕаЮЭГМЦЭМВЙГфЭъећЃЛ
ЃЈ3ЃЉЮЊСЫЙВЭЌНјВНЃЌеХРЯЪІЯыДгБЛЕїВщЕФAРрКЭDРрбЇЩњжаЗжБ№бЁШЁвЛЮЛЭЌбЇНјааЁАвЛАявЛЁБЛЅжњбЇЯАЃЌЧыгУСаБэЗЈЛђЛЪїаЮЭМЕФЗНЗЈЧѓГіЫљбЁСНЮЛЭЌбЇЧЁКУЪЧвЛЮЛФаЭЌбЇКЭвЛЮЛХЎЭЌбЇЕФИХТЪЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЩфЯпBDЪЧЁЯMBNЕФЦНЗжЯпЃЌЕуAЁЂCЗжБ№ЪЧНЧЕФСНБпBMЁЂBNЩЯСНЕуЃЌЧвAB=BCЃЌEЪЧЯпЖЮBCЩЯвЛЕуЃЌЯпЖЮECЕФДЙжБЦНЗжЯпНЛЩфЯпBDгкЕуFЃЌСЌНсAEНЛBDгкЕуGЃЌСЌНсAFЁЂEFЁЂFCЃЎ

ЃЈ1ЃЉЧѓжЄЃКAF=EFЃЛ
ЃЈ2ЃЉЧѓжЄЃКЁїAGFЁзЁїBAFЃЛ
ЃЈ3ЃЉШєЕуPЪЧЯпЖЮAGЩЯвЛЕуЃЌСЌНсBPЃЌШєЁЯPBG=![]() ЁЯBAFЃЌAB=3ЃЌAF=2ЃЌЧѓ
ЁЯBAFЃЌAB=3ЃЌAF=2ЃЌЧѓ![]() ЃЎ
ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌНЋвЛЖЮБъга0ЁЋ60ОљдШПЬЖШЕФЩўзгЦЬЦНКѓелЕўЃЈЩўзгЮоЕЏадЃЉЃЌЪЙЩўзгздЩэЕФвЛВПЗжжиЕўЃЌШЛКѓдкжиЕўВПЗжбиЩўзгДЙжБЗНЯђМєЖЯЃЌНЋЩўзгЗжЮЊAЁЂBЁЂCШ§ЖЮЃЌШєетШ§ЖЮЕФГЄЖШгЩЖЬЕНГЄЕФБШЮЊ1ЃК2ЃК3ЃЌдђелКлЖдгІЕФПЬЖШВЛПЩФмЪЧЃЈЁЁЁЁЃЉ
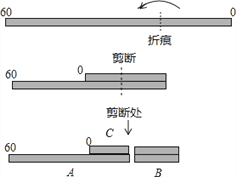
A. 20 B. 25 C. 30 D. 35
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЁЯAOBЪЧЦННЧЃЌODЪЧЁЯAOCЕФНЧЦНЗжЯпЃЌЁЯCOEЃНЁЯBOEЃЎ
ЃЈ1ЃЉШєЁЯAOCЃН 50ЁуЃЌдђЁЯDOEЃН ЁуЃЛ
ЃЈ2ЃЉШєЁЯAOCЃН 50ЁуЃЌдђЭМжагыЁЯCODЛЅВЙЕФНЧЮЊ ЃЛ
ЃЈ3ЃЉЕБЁЯAOCЕФДѓаЁЗЂЩњИФБфЪБЃЌЁЯDOEЕФДѓаЁЪЧЗёЗЂЩњИФБфЃПЮЊЪВУДЃП

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЙлВьЯТСаСНИіЕШЪНЃК2ЁС![]() ЃН22Љ2ЁС
ЃН22Љ2ЁС![]() Љ2ЃЌ4ЁС
Љ2ЃЌ4ЁС![]() ЃН42Љ2ЁС
ЃН42Љ2ЁС![]() Љ2ЃЌИјГіЖЈвхШчЯТЃКЮвУЧГЦЪЙЕШЪНabЃНa2Љ2bЉ2ГЩСЂЕФвЛЖдгаРэЪ§aЃЌbЮЊЁАЗНВюгаРэЪ§ЖдЁБЃЌМЧЮЊЃЈaЃЌbЃЉЃЌШчЃКЃЈ2ЃЌ
Љ2ЃЌИјГіЖЈвхШчЯТЃКЮвУЧГЦЪЙЕШЪНabЃНa2Љ2bЉ2ГЩСЂЕФвЛЖдгаРэЪ§aЃЌbЮЊЁАЗНВюгаРэЪ§ЖдЁБЃЌМЧЮЊЃЈaЃЌbЃЉЃЌШчЃКЃЈ2ЃЌ![]() ЃЉЃЌЃЈ4ЃЌ
ЃЉЃЌЃЈ4ЃЌ![]() ЃЉЖМЪЧЁАЗНВюгаРэЪ§ЖдЁБЃЎ
ЃЉЖМЪЧЁАЗНВюгаРэЪ§ЖдЁБЃЎ
ЃЈ1ЃЉХаЖЯЪ§ЖдЃЈЉ1ЃЌЉ1ЃЉЪЧЗёЮЊЁАЗНВюгаРэЪ§ЖдЁБЃЌВЂЫЕУїРэгЩЃЛ
ЃЈ2ЃЉШєЃЈmЃЌ2ЃЉЪЧЁАЗНВюгаРэЪ§ЖдЁБЃЌЧѓЉ6mЉ3[m2Љ2ЃЈ2mЉ1ЃЉ]ЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЧѓСНЮЛЪ§ЕФЦНЗНЪБЃЌПЩвдгУЁАСаЪњЪНЁБЕФЗНЗЈНјааЫйЫуЃЌЧѓНтЙ§ГЬШчЭМ1ЫљЪОЃЎЗТееЭМ1ЃЌгУЁАСаЪњЪНЁБЕФЗНЗЈМЦЫувЛИіСНЮЛЪ§ЕФЦНЗНЃЌВПЗжЙ§ГЬШчЭМ2ЫљЪОЃЌШєетИіСНЮЛЪ§ЕФИіЮЛЪ§зжЮЊaЃЌдђетИіСНЮЛЪ§ЮЊЃЈЁЁЁЁЃЉ
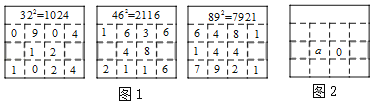
A.aЉ50B.a+50C.aЉ20D.a+20
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМ1ЃЌOЮЊжБЯпABЩЯвЛЕуЃЌЙ§ЕуOзїЩфЯпOCЃЌЁЯAOCЃН30ЁуЃЌНЋвЛжБНЧШ§НЧАхЃЈЦфжаЁЯPЃН30ЁуЃЉЕФжБНЧЖЅЕуЗХдкЕуOДІЃЌвЛБпOQдкЩфЯпOAЩЯЃЌСэвЛБпOPгыOCЖМдкжБЯпABЕФЩЯЗНЃЎНЋЭМ1жаЕФШ§НЧАхШЦЕуOвдУПУы3ЁуЕФЫйЖШбиЫГЪБеыЗНЯђа§зЊвЛжмЃЎ
ЃЈ1ЃЉШчЭМ2ЃЌОЙ§tУыКѓЃЌOPЧЁКУЦНЗжЁЯBOCЃЎ
ЂйЧѓtЕФжЕЃЛ
ЂкДЫЪБOQЪЧЗёЦНЗжЁЯAOCЃПЧыЫЕУїРэгЩЃЛ
ЃЈ2ЃЉШєдкШ§НЧАхзЊЖЏЕФЭЌЪБЃЌЩфЯпOCвВШЦOЕувдУПУы6ЁуЕФЫйЖШбиЫГЪБеыЗНЯђа§зЊвЛжмЃЌШчЭМ3ЃЌФЧУДОЙ§ЖрГЄЪБМфOCЦНЗжЁЯPOQЃПЧыЫЕУїРэгЩЃЛ
ЃЈ3ЃЉдкЃЈ2ЃЉЮЪЕФЛљДЁЩЯЃЌОЙ§ЖрЩйУыOCЦНЗжЁЯPOBЃПЃЈжБНгаДГіНсЙћЃЉЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЩЬЕъОЯњвЛжжНЁЩэЧђЃЌвбжЊетжжНЁЩэЧђЕФГЩБОМлЮЊУПИі20дЊЃЌЪаГЁЕїВщЗЂЯжЃЌИУжжНЁЩэЧђУПЬьЕФЯњЪлСПyЃЈИіЃЉгыЯњЪлЕЅМлxЃЈдЊЃЉгаШчЯТЙиЯЕЃКy=Љ20x+80ЃЈ20ЁмxЁм40ЃЉЃЌЩшетжжНЁЩэЧђУПЬьЕФЯњЪлРћШѓЮЊwдЊЃЎ
ЃЈ1ЃЉЧѓwгыxжЎМфЕФКЏЪ§ЙиЯЕЪНЃЛ
ЃЈ2ЃЉИУжжНЁЩэЧђЯњЪлЕЅМлЖЈЮЊЖрЩйдЊЪБЃЌУПЬьЕФЯњЪлРћШѓзюДѓЃПзюДѓРћШѓЪЧЖрЩйдЊЃП
ЃЈ3ЃЉШчЙћЮяМлВПУХЙцЖЈетжжНЁЩэЧђЕФЯњЪлЕЅМлВЛИпгк28дЊЃЌИУЩЬЕъЯњЪлетжжНЁЩэЧђУПЬьвЊЛёЕУ150дЊЕФЯњЪлРћШѓЃЌЯњЪлЕЅМлгІЖЈЮЊЖрЩйдЊЃП
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com