
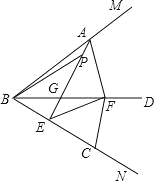
【题目】如图,射线BD是∠MBN的平分线,点A、C分别是角的两边BM、BN上两点,且AB=BC,E是线段BC上一点,线段EC的垂直平分线交射线BD于点F,连结AE交BD于点G,连结AF、EF、FC.

(1)求证:AF=EF;
(2)求证:△AGF∽△BAF;
(3)若点P是线段AG上一点,连结BP,若∠PBG=![]() ∠BAF,AB=3,AF=2,求
∠BAF,AB=3,AF=2,求![]() .
.
【答案】(1)见解析;
(2)见解析;
(3)![]() =
=![]()
【解析】
试题分析:(1)由于EF=CF,要证AF=EF,只需证FA=FC,只需证△ABF≌△CBF即可;
(2)由于∠AFG=∠BFA,要证△AGF∽△BAF,只需证∠FAE=∠ABF,易得∠FAE=∠FEA,∠ABF=∠CBF,只需证∠ABC+∠AFE=180°,只需证∠BAF+∠BEF=180°,只需证到∠BAF=∠FEC即可;
(3)由△AGF∽△BAF可得∠BAF=∠AGF,![]() =
=![]() ,易证△BGE∽△AGF,则有
,易证△BGE∽△AGF,则有![]() =
=![]() ,由条件∠PBG=
,由条件∠PBG=![]() ∠BAF可得∠PBG=
∠BAF可得∠PBG=![]() ∠AGF,由此可得∠BPG=∠PBG,即可得到BG=PG,问题得以解决.
∠AGF,由此可得∠BPG=∠PBG,即可得到BG=PG,问题得以解决.
试题解析: (1)∵BF平分∠ABC,
∴∠ABF=∠CBF.
在△ABF和△CBF中,
BA=BC, ∠ABF=∠CBF,BF=BF,
∴△ABF≌△CBF,
∴AF=CF.
∵点F在EC的垂直平分线上,
∴EF=CF,
∴AF=EF;
(2)∵△ABF≌△CBF,
∴∠BAF=∠BCF.
∵FE=FC,
∴∠FEC=∠FCE,
∴∠BAF=∠FEC.
∵∠BEF+∠FEC=180°,
∴∠BAF+∠BEF=180°.
∵∠BAF+∠ABE+∠BEF+∠AFE=360°,
∴∠ABE+∠AFE=180°.
∵FA=FE,
∴∠FAE=∠FEA.
∵∠AFE+∠FAE+∠FEA=180°,
∴∠ABE=∠FAE+∠FEA=2∠FAE.
又∵∠ABE=2∠ABF,
∴∠FAE=∠ABF.
∵∠AFG=∠BFA,
∴△AGF∽△BAF;
(3)∵△AGF∽△BAF,
∴∠AGF=∠BAF,![]() .
.
∵∠PBG=![]() ∠BAF,AB=3,AF=2,
∠BAF,AB=3,AF=2,
∴∠PBG=![]() ∠AGF,
∠AGF,![]() =
=![]() ,
,
∴∠BPG=∠PBG,![]() =
=![]() ,
,
∴PG=BG,
∴![]() .
.
∵∠GAF=∠ABF=∠EBF,∠AGF=∠BGE,
∴△BGE∽△AGF,
∴![]() =
=![]() ,
,
∴![]() =
=![]() .
.


 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:初中数学 来源: 题型:
【题目】已知关于x,y的方程组![]() ,则下列结论中正确的是( )
,则下列结论中正确的是( )
①当a=5时,方程组的解是![]() ;
;
②当x,y的值互为相反数时,a=20;
③不存在一个实数a使得x=y;
④若![]() ,则a=2.
,则a=2.
A. ①②③④ B. ②③ C. ②③④ D. ②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题背景:
如图1,△ABC为等边三角形,作AD⊥BC于点D,将∠ABC绕点B顺时针旋转30°后,BA,BC边与射线AD分别交于点E,F,求证:△BEF为等边三角形.
迁移应用:
如图2,△ABC为等边三角形,点P是△ABC外一点,∠BPC=60°,将∠BPC绕点P逆时针旋转60°后,PC边恰好经过点A,探究PA,PB,PC之间存在的数量关系,并证明你的结论;
拓展延伸:
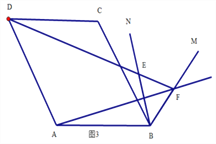
如图3,在菱形ABCD中,∠ABC=60°,将∠ABC绕点B顺时针旋转到如图所在的位置得到∠MBN,F是BM上一点,连接AF,DF,DF交BN于点E,若B,E两点恰好关于直线AF对称.
(1)证明△BEF是等边三角形;
(2)若DE=6,BE=2,求AF的长.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正方形A1B1C1O、A2B2C2C1、A3B3C3C2、……按如图的方式放置,点A1、A2、A3……和点C1、C2、C3……分别在直线y=x+1和x轴上,则点B6的坐标是( )
A. (31,16) B. (63,32) C. (15,8) D. (31,32)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图在Rt△ABC中,∠ACB=90°,D是边AB的中点,BE⊥CD,垂足为点E.已知AC=15,cosA=![]() .
.
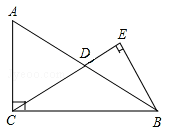
(1)求线段CD的长;
(2)求sin∠DBE的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,M、N分别是边AD、BC边上的中点,且△ABM≌△DCM;E、F分别是线段BM、CM的中点.
(1)求证:平行四边形ABCD是矩形.
(2)求证:EF与MN互相垂直.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,数轴上表示1、![]() 的对应点分别为A、B,点C在OA上,且AC=AB,试求点C所表示的实数.
的对应点分别为A、B,点C在OA上,且AC=AB,试求点C所表示的实数.

(2)如图2,数轴的正半轴上有A、B、C三点,表示1和![]() 的对应点分别为A、B,点B到点A的距离与点C到点O的距离相等,设点C所表示的数为x.求(x﹣
的对应点分别为A、B,点B到点A的距离与点C到点O的距离相等,设点C所表示的数为x.求(x﹣![]() )2的立方根.
)2的立方根.
(3)如图3,a,b,c是数轴上三个点A、B、C所对应的实数.(|c|>|b|>|a|),试化简:![]()
![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电信公司有甲、乙两种手机收费业务,仅上网流量收费不同,图中I1、I2分别表示甲、乙两种业务每月流量费用y(元)与上网流量xGB的之间的函数关系。

(1)分别求出甲、乙两种业务每月所收费用y元与上网流量xGB之间的函数关系式。
(2)已知刘老师选择了甲业务,魏老师选择了乙业务,上月两位老师所用流量相同,均为mGB,上网流量费用相差不到20元,求m的取值范围。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察算式:1×3+1=4=22;2×4+1=9=32;3×5+1=16=42;4×6+1=25=52,…
(1)请根据你发现的规律填空:6×8+1=( )2;
(2)用含n的等式表示上面的规律: ;
(3)用找到的规律解决下面的问题:
计算:(1+![]() )(1+
)(1+![]() )(1+
)(1+![]() )(1+
)(1+![]() )…(1+
)…(1+![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com