
分析 根据整式的混合运算可以将题目中的问题进行解答,第(3)个式子可以通过变形,利用平方差公式进行计算.
解答 解:(1)(-2a2b)2•3ab3÷(-6a3b)
=4a4b2×3ab3÷(-6a3b)
=-(4×3÷6)a4+1-3b2+3-1
=-2a2b4;
(2)(5mn2-4m2n)(-2mn)
=5mn2×(-2mn)-4m2n×(-2mn)
=-10m2n3+8m3n2;
(3)20102-2009×2011(利用公式)
=20102-(2010-1)(2010+1)
=20102-(20102-1)
=20102-20102+1
=1;
(4)(2x+3)(x-4)-2(x+2)(x-3)
=2x2-5x-12-(2x2-2x-12)
=2x2-5x-12-2x2+2x+12
=-3x.
点评 本题考查整式的混合运算,解题的关键是明确同底数幂的乘除法法则,平方差公式的应用.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
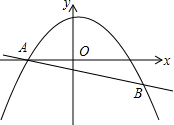 如图,抛物线${y_1}=-\frac{1}{4}{x^2}+\frac{1}{4}x+3$与直线${y_2}=-\frac{1}{4}x-\frac{3}{4}$交于A、B两点,则使y1≥y2成立的x取值范围是-2≤x≤5.
如图,抛物线${y_1}=-\frac{1}{4}{x^2}+\frac{1}{4}x+3$与直线${y_2}=-\frac{1}{4}x-\frac{3}{4}$交于A、B两点,则使y1≥y2成立的x取值范围是-2≤x≤5.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
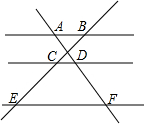 如图,已知AB∥CD∥EF,那么下列结论不正确的是( )
如图,已知AB∥CD∥EF,那么下列结论不正确的是( )| A. | $\frac{AD}{DF}=\frac{BC}{CE}$ | B. | $\frac{BC}{CE}$=$\frac{DF}{AD}$ | C. | $\frac{CE}{EB}=\frac{DF}{AF}$ | D. | $\frac{BC}{BE}=\frac{AD}{AF}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com