
【题目】如图所示,抛物线y=x2﹣4x+3与x轴分别交于A、B两点,交y轴于点C,
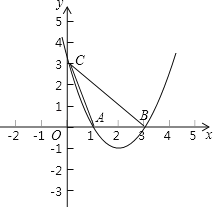
(1)求cos∠CAO的值;
(2)求直线AC的函数关系式;
(3)如果有动点P是y轴上,且△OPA与△OAC相似,求P点坐标.
【答案】(1)cos∠CAO=![]() ;(2)直线AC的解析式为:y=﹣3x+3;(3)点P的坐标为:(0,﹣3),(0,
;(2)直线AC的解析式为:y=﹣3x+3;(3)点P的坐标为:(0,﹣3),(0,![]() ),(0,﹣
),(0,﹣![]() ).
).
【解析】
试题分析:(1)根据抛物线y=x2﹣4x+3与x轴分别交于A、B两点,交y轴于点C,可以求得A、B、C三点的坐标,从而可以求得OA、OC、AC的长,进而可以得到cos∠CAO的值;
(2)根据点A、C两点的坐标,可以求得直线AC的函数关系式;
(3)根据第三问的条件,可知符合要求的三角形OPA存在三种情况,然后分别画出相应的图形,即可求得点P的坐标.
解:(1)∵抛物线y=x2﹣4x+3与x轴分别交于A、B两点,交y轴于点C,
∴x2﹣4x+3=0,得x=1或x=3,x=0时,y=3,
∴点A的坐标为(1,0),点B的坐标为(3,0),点C的坐标为(0,3),
∴OA=1,OC=3,
∴![]() ,
,
∴cos∠CAO=![]() ;
;
(2)设直线AC的解析式为:y=kx+b,
∵点A的坐标为(1,0),点C的坐标为(0,3),
∴![]()
解得k=﹣3,b=3.
即直线AC的解析式为:y=﹣3x+3;
(3)如果有动点P是y轴上,且△OPA与△OAC相似,
则有如下三种情况,
第一种情况如下图1所示,
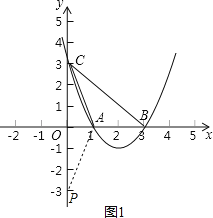
当∠OPA=∠OCA,∠AOC=∠AOP时,△OPA∽△OAC,
∴![]() ,
,
∵点C的坐标为(0,3),
∴OP=OC=3,
∴点P的坐标为(0,﹣3);
第二种情况如下图2所示,点P位于y轴正半轴,
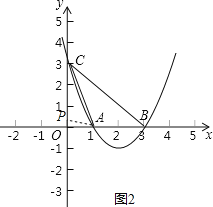
当∠OPA=∠OAC,∠AOC=∠AOP时,△OPA∽△OAC,
∴![]() ,
,
∵点C的坐标为(0,3),点A的坐标为(1,0),
∴OA=1,OC=3,
∴![]() ,
,
即点P的坐标为(0,![]() );
);
第三种情况如下图3所示,点P位于y轴负半轴,
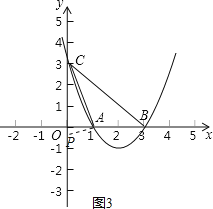
当∠OPA=∠OAC,∠AOC=∠AOP时,△OPA∽△OAC,
∴![]() ,
,
∵点C的坐标为(0,3),点A的坐标为(1,0),
∴OA=1,OC=3,
∴![]() ,
,
即点P的坐标为(0,﹣![]() ).
).
由上可得,点P的坐标为:(0,﹣3),(0,![]() ),(0,﹣
),(0,﹣![]() ).
).


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,已知∠AOB=120°,射线OA绕点O以每秒钟6°的速度逆时针旋转到OP,设射线OA旋转OP所用时间为t秒(t<30).
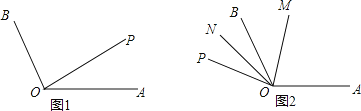
(1)如图1,直接写出∠BOP= °(用含t的式子表示);
(2)若OM平分∠AOP,ON平分∠BOP.
①当OA旋转到如图1所示OP处,请完成作图并求∠MON的度数;
②当OA旋转到如图2所示OP处,若2∠BOM=3∠BON,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一次函数y=﹣2x的图象与反比例函数y=![]() 的图象交于点A(﹣1,n).
的图象交于点A(﹣1,n).
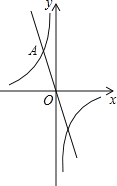
(1)求反比例函数y=![]() 的解析式;
的解析式;
(2)若P是x轴上一点,且△AOP是等腰三角形,求点P的坐标;
(3)结合图象直接写出不等式![]() +2x>0的解集为 .
+2x>0的解集为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC的内切圆⊙O与两直角边AB,BC分别相切于点D,E,过劣弧![]() (不包括端点D,E)上任一点P作⊙O的切线MN与AB,BC分别交于点M,N,若⊙O的半径为r,则Rt△MBN的周长为( )
(不包括端点D,E)上任一点P作⊙O的切线MN与AB,BC分别交于点M,N,若⊙O的半径为r,则Rt△MBN的周长为( )

A.r B.![]() r C.2r D.
r C.2r D.![]() r
r
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果Rt△ABC中各边的长度都扩大到原来的2倍,那么锐角∠A的三角比的值( )
A.都扩大到原来的2倍
B.都缩小到原来的一半
C.没有变化
D.不能确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一长方形的一边长为5a一6b,另一边比它小3a一b,则它的周长是( )
A. 14a一22b B. 14a+22b C. 7a+11b D. 7a一11b
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com