
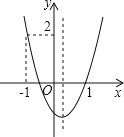
【题目】如图,二次函数![]() 的图象开口向上,图象经过点(-1,2)和(1,0),且与y
的图象开口向上,图象经过点(-1,2)和(1,0),且与y
轴相交于负半轴。给出四个结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ,其中正确结论的序
,其中正确结论的序
号是___________
【答案】②③④.
【解析】由抛物线的开口方向判断a与0的关系,由抛物线与y轴的交点判断c与0的关系,然后根据对称轴及抛物线与x轴交点情况进行推理,进而对所得结论进行判断.
解:(1)①由抛物线的开口方向向上可推出a>0,正确;
②因为对称轴在y轴右侧,对称轴为x=-![]() >0,又因为a>0,∴b<0,错误;
>0,又因为a>0,∴b<0,错误;
③由抛物线与y轴的交点在y轴的负半轴上,∴c<0,错误;
④由图象可知:当x=1时y=0,∴a+b+c=0,正确.
故(1)中,正确结论的序号是①④.
(2)①∵a>0,b<0,c<0,∴abc>0,错误;
②由图象可知:对称轴x=-![]() >0且对称轴x=-
>0且对称轴x=-![]() <1,∴2a+b>0,正确;
<1,∴2a+b>0,正确;
③由图象可知:当x=-1时y=2,∴a-b+c=2,当x=1时y=0,∴a+b+c=0;
a-b+c=2与a+b+c=0相加得2a+2c=2,解得a+c=1,正确;
④∵a+c=1,移项得a=1-c,又∵c<0,∴a>1,正确.
故(2)中,正确结论的序号是②③④.
“点睛”二次函数y=ax2+bx+c系数符号的确定:(1)a由抛物线开口方向确定:开口方向向上,则a>0;否则a<0.(2)b由对称轴和a的符号确定:由对称轴公式x=-![]() 判断符号.(3)c由抛物线与y轴的交点确定:交点在y轴正半轴,则c>0;否则c<0.(4)b2-4ac由抛物线与x轴交点的个数确定:2个交点,b2-4ac>0;1个交点,b2-4ac=0;没有交点,b2-4ac<0.
判断符号.(3)c由抛物线与y轴的交点确定:交点在y轴正半轴,则c>0;否则c<0.(4)b2-4ac由抛物线与x轴交点的个数确定:2个交点,b2-4ac>0;1个交点,b2-4ac=0;没有交点,b2-4ac<0.


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=4,AC=3.
(1)试在AB上确定点D的位置,△ACD∽△ABC;
(2)试在AC的延长线上确定点E的位置,使△AEB∽△ABC,此时BE与DC有怎样的位置关系?为什么?

查看答案和解析>>
科目:初中数学 来源: 题型:
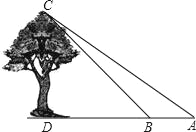
【题目】在数学活动课上,九年级(1)班数学兴趣小组的同学们测量校园内一棵大树(如图)的高度,设计的方案及测量数据如下:(1)在大树前的平地上选择一点A,测得由点A看大树顶端C的仰角为35°;(2)在点A和大树之间选择一点B(A,B,D在同一直线上),测得由点B看大树顶端C的仰角恰好为45°;(3)量出A,B两点间的距离为4.5米.请你根据以上数据求出大树CD的高度.(精确到0.1米)(可能用到的参考数据sin35°≈0.57cos35°≈0.82,tan35°≈0.70)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市销售一种商品,成本每千克40元,规定每千克售价不低于成本,且不高于80元,经市场调查,每天的销售量y(千克)与每千克售价x(元)满足一次函数关系,部分数据如下表:
售价x(元/千克) | 50 | 60 | 70 |
销售量y(千克) | 100 | 80 | 60 |
(1)求y与x之间的函数表达式;
(2)设商品每天的总利润为W(元),则当售价x定为多少元时,厂商每天能获得最大利润?最大利润是多少?
(3)如果超市要获得每天不低于1350元的利润,且符合超市自己的规定,那么该商品每千克售价的取值范围是多少?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB和抛物线的交点是A(0,-3),B(5,9),已知抛物线的顶点D的横坐标是2.

(1)求抛物线的解析式及顶点坐标;
(2)在![]() 轴上是否存在一点C,与A,B组成等腰三角形?若存在,求出点C的坐标,若不存在,请说明理由;
轴上是否存在一点C,与A,B组成等腰三角形?若存在,求出点C的坐标,若不存在,请说明理由;
(3)在直线AB的下方抛物线上找一点P,连接PA,PB使得△PAB的面积最大,并求出这个最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=x2﹣mx+m﹣2:
(1)求证:不论m为任何实数,此二次函数的图象与x轴都有两个交点;
(2)当二次函数的图象经过点(3,6)时,确定m的值,并写出此二次函数与坐标轴的交点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】求证:相似三角形对应边上的中线之比等于相似比.
要求:①根据给出的△ABC及线段A'B′,∠A′(∠A′=∠A),以线段A′B′为一边,在给出的图形上用尺规作出△A'B′C′,使得△A'B′C′∽△ABC,不写作法,保留作图痕迹;
②在已有的图形上画出一组对应中线,并据此写出已知、求证和证明过程.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=(t+1)x2+2(t+2)x+![]() 在x=0和x=2时的函数值相等
在x=0和x=2时的函数值相等
(1)求二次函数的解析式,并作图象;
(2)若一次函数y=kx+6的图象与二次函数的象都经过点A(﹣3,m),求m和k的值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com