
【题目】一慢车和一快车沿相同路线从A地到B地,所行的路程与时间的图象如图所示,试根据图象,回答下列问题:
(1)慢车比快车早出发______小时,快车追上慢车时行驶了_____千米,快车比慢车早______小时到达B地;
(2)求慢车、快车的速度;
(3)快车追上慢车需几个小时?

科目:初中数学 来源: 题型:
【题目】一个钢筋三角架三边长分别为20cm,50cm,60cm,现要再做一个与其相似的钢筋三角架,而只有长为30cm和50cm的两根钢筋,要求以其中的一根为一边,从另一根截下两段(允许有余料)作为另两边,则不同的截法有( ).
A. 一种 B. 两种 C. 三种 D. 四种
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】射击队为从甲、乙两名运动员中选拔一人参加比赛,对他们进行了六次测试,测试成绩如下表(单位:环):
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六次 | 平均成绩 | 中位数 | |
甲 | 10 | 8 | 9 | 8 | 10 | 9 | 9 | ① |
乙 | 10 | 7 | 10 | 10 | 9 | 8 | ② | 9.5 |
(注:方差公式 ![]() .)
.)
(1)完成表中填空①;②;
(2)请计算甲六次测试成绩的方差;
(3)若乙六次测试成绩的方差为 ![]() ,你认为推荐谁参加比赛更合适,请说明理由.
,你认为推荐谁参加比赛更合适,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读与应用:
阅读1:a、b为实数,且a>0,b>0,因为 ![]() ,所以
,所以 ![]() ,从而
,从而 ![]() (当a=b时取等号).
(当a=b时取等号).
阅读2:函数 ![]() (常数m>0,x>0),由阅读1结论可知:
(常数m>0,x>0),由阅读1结论可知: ![]()
![]() ,所以当
,所以当 ![]() 即
即 ![]() 时,函数
时,函数 ![]() 的最小值为
的最小值为 ![]() .
.
阅读理解上述内容,解答下列问题:
(1)问题1:已知一个矩形的面积为4,其中一边长为x,则另一边长为 ![]() ,周长为
,周长为 ![]() ,求当x=时,周长的最小值为 .
,求当x=时,周长的最小值为 .
(2)问题2:已知函数y1=x+1(x>-1)与函数y2=x2+2x+17(x>-1),当x=时, ![]() 的最小值为 .
的最小值为 .
(3)问题3:某民办学习每天的支出总费用包含以下三个部分:一是教职工工资6400元;二是学生生活费每人10元;三是其他费用.其中,其他费用与学生人数的平方成正比,比例系数为0.01.当学校学生人数为多少时,该校每天生均投入最低?最低费用是多少元?(生均投入=支出总费用÷学生人数)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,AC、BD交于点O,BD⊥AD于点D,将△ABD沿BD翻折得到△EBD,连接EC、EB.
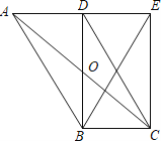
(1)求证:四边形DBCE是矩形;
(2)若BD=4,AD=3,求点O到AB的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,直线MN与直线AB、CD分别交于点E、F,∠1与∠2互补.
(1)试判断直线AB与直线CD的位置关系,并说明理由;
(2)如图2,∠BEF与∠EFD的角平分线交于点P,EP与CD交于点G,点H是MN上一点,且GH⊥EG,求证:PF∥GH;
(3)如图3,在(2)的条件下,连接PH,K是GH上一点使∠PHK=∠HPK,作PQ平分∠EPK,问∠HPQ的大小是否发生变化?若不变,请求出其值;若变化,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,![]() 的四个顶点分别为
的四个顶点分别为![]() ,
,![]() ,
,![]() ,
,![]() .
.
(1)作![]() ,使它与
,使它与![]() 关于原点
关于原点![]() 成中心对称.
成中心对称.
(2)作![]() 的两条对角线的交点
的两条对角线的交点![]() 关于
关于![]() 轴的对称点
轴的对称点![]() ,点
,点![]() 的坐标为_______.
的坐标为_______.
(3)若将点![]() 向上平移
向上平移![]() 个单位,使其落在
个单位,使其落在![]() 内部(不包括边界),则
内部(不包括边界),则![]() 的取值范围是_______.
的取值范围是_______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】制作一种产品,需先将材料加热达到60 ℃后,再进行操作.设该材料温度为y(℃),从加热开始计算的时间为x(min).据了解,当该材料加热时,温度y与时间x成一次函数关系;停止加热进行操作时,温度y与时间x成反比例关系(如图).已知该材料在操作加热前的温度为15 ℃,加热5分钟后温度达到60 ℃.

(1)分别求出将材料加热和停止加热进行操作时,y与x的函数关系式;
(2)根据工艺要求,当材料的温度低于15 ℃时,须停止操作,那么从开始加热到停止操作,共经历了多少时间?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com