
【题目】如图,矩形![]() 中,
中,![]() 为
为![]() 中点,过点
中点,过点![]() 的直线分别与
的直线分别与![]() ,
,![]() 交于点
交于点![]() ,
,![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,
,![]() .若
.若![]() ,
,![]() ,则下列结论:
,则下列结论:
①![]() ,
,![]() ;
;
②![]() ;
;
③四边形![]() 是菱形;
是菱形;
④![]() .
.
其中正确结论的个数是( )

A. 1 B. 2 C. 3 D. 4
【答案】C
【解析】
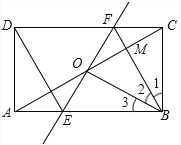
①证明△OBC是等边三角形,即可得OB=BC,由FO=FC,即可得FB垂直平分OC,①正确;②由FB垂直平分OC,根据轴对称的性质可得△FCB≌△FOB,根据全等三角形的性质可得∠BCF=∠BOF=90°,再证明△FOC≌△EOA,所以FO=EO,即可得OB垂直平分EF,所以△OBF≌△OBE,即△EOB≌△FCB,②错误;③证明四边形DEBF是平行四边形,再由OB垂直平分EF,根据线段垂直平分线的性质可得BE=BF,即可得平行四边形DEBF为菱形,③正确;④由OBF≌△EOB≌△FCB得∠1=∠2=∠3=30°,在Rt△OBE中,可得OE =![]() OB,在Rt△OBM中,可得BM=
OB,在Rt△OBM中,可得BM=![]() OB,即可得BM :OE =3:2,④正确.
OB,即可得BM :OE =3:2,④正确.
①∵矩形ABCD中,O为AC中点,
∴OB=OC,
∵∠COB=60°,
∴△OBC是等边三角形,
∴OB=BC,
∵FO=FC,
∴FB垂直平分OC,
∴FB⊥OC,OM=CM;
①正确;
②∵FB垂直平分OC,
根据轴对称的性质可得△FCB≌△FOB,
∴∠BCF=∠BOF=90°,即OB⊥EF,
∵OA=OC,∠FOC=∠EOA,∠DCO=∠BAO,
∴△FOC≌△EOA,
∴FO=EO,
∴OB垂直平分EF,
∴△OBF≌△OBE,
∴△EOB≌△FCB,
②错误;
③∵△FOC≌△EOA,
∴FC=AE,
∵矩形ABCD,
∴CD=AB,CD∥AB,
∴DF∥EB,DF=EB,
∴四边形DEBF是平行四边形,
∵OB垂直平分EF,
∴BE=BF,
∴平行四边形DEBF为菱形;
③正确;
④由OBF≌△EOB≌△FCB得∠1=∠2=∠3=30°,
在Rt△OBE中,OE =![]() OB,
OB,
在Rt△OBM中,BM=![]() OB,
OB,
∴BM :OE =![]() OB:=
OB:=![]() OB=3:2.
OB=3:2.
④正确;
所以其中正确结论的个数为3个;
故选C.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
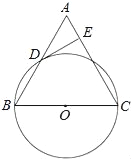
【题目】已知:如图,在△ABC中,BC=AC,以BC为直径的⊙O与边AB相交于点D,DE⊥AC,垂足为点E.
(1)求证:点D是AB的中点;
(2)判断DE与⊙O的位置关系,并证明你的结论;
(3)若⊙O的直径为18,cosB=![]() ,求DE的长.
,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践
问题解决:
如图1,已知正方形![]() ,
,![]() ,把含
,把含![]() (
(![]() )的直角三角板的一个锐角顶点和点
)的直角三角板的一个锐角顶点和点![]() 重合,三角板和正方形的
重合,三角板和正方形的![]() ,
,![]() 两边分别相交于
两边分别相交于![]() ,
,![]() 两点.
两点.
(1)当![]() 时,求
时,求![]() 的长;
的长;
探究发现:
(2)在图1的基础上,试探究![]() ,
,![]() ,
,![]() 有怎样的数量关系,请写出猜想,并给予证明.
有怎样的数量关系,请写出猜想,并给予证明.
类比延伸:
(3)如图2,若三角板和正方形![]() ,
,![]() 两边的延长线分别相交于
两边的延长线分别相交于![]() ,
,![]() 两点,请直接写出
两点,请直接写出![]() ,
,![]() ,
,![]() 存在的数量关系.
存在的数量关系.


查看答案和解析>>
科目:初中数学 来源: 题型:
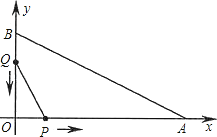
【题目】如图,在平面直角坐标系中,已知OA=12厘米,OB=6厘米.点P从点O开始沿OA边向点A以1厘米/秒的速度移动;点Q从点B开始沿BO边向点O以1厘米/秒的速度移动.如果P、Q同时出发,用t(秒)表示移动的时间(0≤t≤6),那么,当t为何值时,△POQ与△AOB相似?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两班举行电脑汉字输入比赛,参赛学生每分输入汉字的个数统计结果如下表:
班级 | 参加人数 | 中位数 | 方差 | 平均数 |
甲 | 55 | 149 | 1.91 | 135 |
乙 | 55 | 151 | 1.10 | 135 |
某同学分析上表后得到如下结论:
①甲、乙两班学生平均成绩相同;
②乙班优秀的人数多于甲班优秀的人数(每分输入汉字个数![]() 为优秀)
为优秀)
③甲班成绩的波动比乙班大.
上述结论中正确的是( )
A.①②③B.①②C.①③D.②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司有A、B两种型号的客车共11辆,它们的载客量(不含司机)、日租金、车辆数如下表所示,已知这11辆客车满载时可搭载乘客350人.
A型客车 | B型客车 | |
载客量(人/辆) | 40 | 25 |
日租金(元/辆) | 320 | 200 |
车辆数(辆) | a | b |
(1)求a、b的值;
(2)某校七年级师生周日集体参加社会实践,计划租用A、B两种型号的客车共6辆,且租车总费用不超过1700元.
①最多能租用A型客车多少辆?
②若七年级师生共195人,写出所有的租车方案,并确定最省钱的租车方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
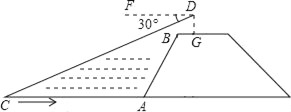
【题目】如图,小华站在河岸上的G点,看见河里有一小船沿垂直于岸边的方向划过来.此时测得小船C的俯角是∠FDC=30°.若小华的眼睛与地面的距离是![]() 米,BG=1.5米,BG平行于AC所在的直线,迎水坡i=4:3,坡长AB=10米,点A、B、C、D、F、G在同一平面内,则此时小船C到岸边的距离CA的长是多少?(结果保留根号)
米,BG=1.5米,BG平行于AC所在的直线,迎水坡i=4:3,坡长AB=10米,点A、B、C、D、F、G在同一平面内,则此时小船C到岸边的距离CA的长是多少?(结果保留根号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com