
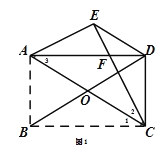
【题目】如图1,矩形ABCD的对角线AC与BD相交于点O,将矩形沿对角线AC折叠,折叠后点B落在点E处,CE交AD于点F,连接DE.
(1)求证:![]() ;
;
(2)当AB与BC满足什么数量关系时,四边形AODE是菱形?请说明理由;
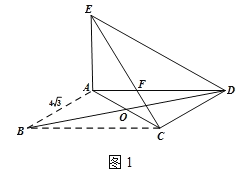
(3)将图1中的矩形ABCD改为平行四边形ABCD,其它条件不变,如图2,若AB=![]() ,∠ABC=30°,点E在直线AD上方,试探究:△AED是直角三角形时,BC的长度是多少.
,∠ABC=30°,点E在直线AD上方,试探究:△AED是直角三角形时,BC的长度是多少.

【答案】(1)证明见解析;(2)当![]() 时,四边形ABCD是菱形,理由见解析;(3)BC=12或8.
时,四边形ABCD是菱形,理由见解析;(3)BC=12或8.
【解析】
(1)根据折叠的性质和平行线的判定定理,即可解答;
(2)先利用折叠的性质,证明四边形AODE是平行四边形,再利用菱形的判定定理即可解答;
(3)根据折叠的性质,再分两种情况进行讨论即可解答.
(1)∵矩形ABCD沿AC折叠
∴∠1=∠2
∵AD∥BC
∴∠1=∠3
∴∠2=∠3
∴AF=CF
∵AD=BC,BC=CE,
∴AD=CE,
∴AD-AF=CE-CF
即EF=DF,
∴∠FED=∠FDE
∵∠AFC=∠EFD,
∴∠3=∠ADE,
∴AC∥DE
(2)当![]() 时,四边形ABCD是菱形.
时,四边形ABCD是菱形.
理由如下:∵在Rt△ABC中,![]()
∴∠1=30°
∴∠3=∠1=30°,∠BAO=60°
∵矩形ABCD沿AC折叠
∴∠BAO=∠CAE=60°
在矩形ABCD中,OA=DO
∴∠3=∠ADO=30°
∴∠EAD=∠CAE-∠3=30°
∴∠EAD=∠ADO
∴AE∥OD
由(1)可知AC∥DE,
∴四边形AODE是平行四边形
又∵OA=DO,
∴四边形AODE是菱形
(3)∵沿AC折叠,
∴∠ACB=∠ACE,BC=CE
∵AD∥BC,
∴∠DAC=∠ACB,
∴∠DAC=∠ACE,
∴FA=FC
∵AD=BC,BC=CE,
∴AD=CE,
∴AD-FA=CE-FC
即EF=DF
①![]() 时,如图1,依题可知
时,如图1,依题可知
![]() ,
,![]()
在![]() 中,
中,![]()
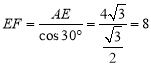 ,
,
∴![]() ,
,
∴![]() .
.
②如图2,当![]() 时,
时,
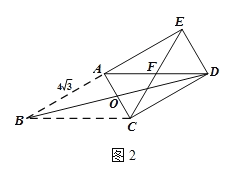
∵∠AEC=∠ABC=30°,
∴∠FED=60°
∵EF=FD,
∴∠FDE=∠FED=60°
在Rt△AED中,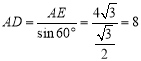 ,
,
∴![]()
综上可知:当点E在直线AD上方时,BC=12或8.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
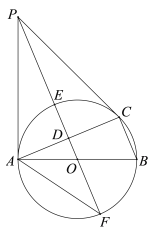
【题目】如图,⊙O是△ABC的外接圆,AB是直径,D是AC中点,直线OD与⊙O相交于E,F两点,P是⊙O外一点,P在直线OD上,连接PA,PC,AF,且满足∠PCA=∠ABC.
(1)求证:PA是⊙O的切线;
(2)证明:![]() ;
;
(3)若BC=8,tan∠AFP=![]() ,求DE的长.
,求DE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,D是AB上一点,以点D为圆心,AC为半径画弧交BA的延长线于点E,连接CD,作EF∥CD,交∠EAC的平分线于点F,连接CF.
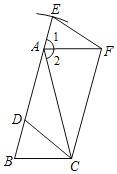
(1)求证:△BCD≌△AFE;
(2)若AC=6,∠BAC=30°,求四边形CDEF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
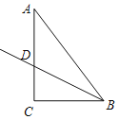
【题目】如图,已知△ABC中,∠C=90°,BC=3,AC=4,BD平分∠ABC,将△ABC绕着点A旋转后,点B、C的对应点分别记为B1、C1,如果点B1落在射线BD上,那么CC1的长度为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知动点A在函数![]() (x>0)的图象上,AB⊥x轴于点B,AC⊥y轴于点C,延长CA,交以A为圆心,AB为半径的圆弧于点D;延长BA,交以A为圆心,AC为半径的圆弧于点E.直线DE分别交x,y轴于点P,Q,当QE:DP=4:9时,图中阴影部分的面积等于____.
(x>0)的图象上,AB⊥x轴于点B,AC⊥y轴于点C,延长CA,交以A为圆心,AB为半径的圆弧于点D;延长BA,交以A为圆心,AC为半径的圆弧于点E.直线DE分别交x,y轴于点P,Q,当QE:DP=4:9时,图中阴影部分的面积等于____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校准备租用一批汽车,现有甲、乙两种大客车,甲种客车每辆载客量45人,乙种客车每辆载客量30人,已知1辆甲种客车和3辆乙种客车共需租金1240元,3辆甲种客车和2辆乙种客车共需租金1760元.
(1)求1辆甲种客车和1辆乙种客车的租金分别是多少元?
(2)学校计划租用甲、乙两种客车共8辆,送330名师生集体外出活动,最节省的租车费用是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,若点
中,若点![]() 和点
和点![]() 关于
关于![]() 轴对称,点
轴对称,点![]() 和点
和点![]() 关于直线
关于直线![]() 对称,则称点
对称,则称点![]() 是点
是点![]() 关于
关于![]() 轴,直线
轴,直线![]() 的二次对称点.
的二次对称点.
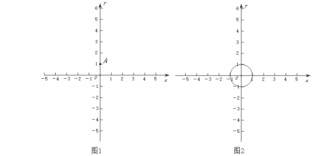
(1)如图1,点![]() .
.
①若点![]() 是点
是点![]() 关于
关于![]() 轴,直线
轴,直线![]() :
:![]() 的二次对称点,则点
的二次对称点,则点![]() 的坐标为________;
的坐标为________;
②若点![]() 是点
是点![]() 关于
关于![]() 轴,直线
轴,直线![]() :
:![]() 的二次对称点,则
的二次对称点,则![]() 的值为_______;
的值为_______;
③若点![]() 是点
是点![]() 关于
关于![]() 轴,直线
轴,直线![]() 的二次对称点,则直线
的二次对称点,则直线![]() 的表达式为__________;
的表达式为__________;
(2)如图2,![]() 的半径为1.若
的半径为1.若![]() 上存在点
上存在点![]() ,使得点
,使得点![]() 是点
是点![]() 关于
关于![]() 轴,直绩
轴,直绩![]() :
:![]() 的二次对称点,且点
的二次对称点,且点![]() 在射线
在射线![]() 上,
上,![]() 的取值范围是________;
的取值范围是________;
(3)![]() 是
是![]() 轴上的动点,
轴上的动点,![]() 的半径为2,若
的半径为2,若![]() 上存在点
上存在点![]() ,使得点
,使得点![]() 是点
是点![]() 关于
关于![]() 轴,直线
轴,直线![]() :
:![]() 的二次对称点,且点
的二次对称点,且点![]() 在
在![]() 轴上,求
轴上,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com