
ЁОЬтФПЁПШчЭМЃЌдкжБНЧзјБъЯЕжаЃЌOC ODЃЌOC OD ЃЌDC ЕФбгГЄЯпНЛ y жсе§АыжсЩЯЕу B ЃЌЙ§ЕуC зїCA BD НЛ x жсИКАыжсгкЕуA ЃЎ
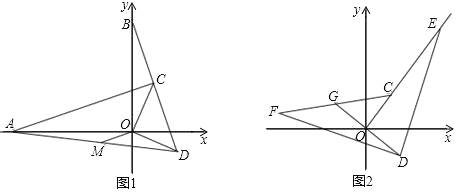
ЃЈ1ЃЉШчЭМ1ЃЌЧѓжЄЃКOAOB
ЃЈ2ЃЉШчЭМ1ЃЌСЌADЃЌзїOM ЁЮACНЛADгкЕуMЃЌЧѓжЄЃК BC 2OM
ЃЈ3ЃЉШчЭМ2ЃЌЕуEЮЊOC ЕФбгГЄЯпЩЯвЛЕуЃЌСЌDEЃЌЙ§ЕуDзїDFDEЧвDF DE ЃЌСЌCF НЛ DO ЕФбгГЄЯпгкЕуG ШєOG 4ЃЌЧѓCE ЕФГЄЃЎ
ЁОД№АИЁПЃЈ1ЃЉМћНтЮіЃЛЃЈ2ЃЉМћНтЮіЃЛЃЈ3ЃЉCE=OT=8ЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉгЩOCЁЭODЃЌCAЁЭBDжЊЁЯCOD=ЁЯBCA=ЁЯAOB=90ЁуЃЌДгЖјЕУЁЯAOC=ЁЯBODЃЌЁЯOBD=ЁЯOACЃЌНсКЯOC=ODжЄЁїAOCЁеЁїBODПЩЕУД№АИЃЛ
ЃЈ2ЃЉзїANЁЮODЃЌНЛOMбгГЄЯпгкЕуNЃЌЯШжЄЁїBOCЁеЁїOANЕУBC=ONЃЌAN=OC=ODЃЌдйжЄЁїAMNЁеЁїDMOЕУOM=MN=![]() ONЃЌДгЖјЕУжЄЃЛ
ONЃЌДгЖјЕУжЄЃЛ
ЃЈ3ЃЉзїFTЁЭDGЃЌНЛDGбгГЄЯпгкЕуTЃЌЯШжЄЁїFTDЁеЁїDOEЕУFT=OD=OCЃЌDT=OEЃЌдйжЄЁїFTGЁеЁїCOGЕУOT=2OG=8ЃЌИљОнOE=DTЃЌOC=ODПЩЕУCE=OTЃЎ
НтЃКЃЈ1ЃЉЁпOCЁЭODЃЌCAЁЭBDЃЌ
ЁрЁЯCOD=ЁЯBCA=ЁЯAOB=90ЁуЃЌ
ЁрЁЯBOC+ЁЯCOE=90Ёу, ЁЯDOE+ЁЯCOE=90Ёу,
ЁрЁЯBOC=ЁЯDOE,
ЁрЁЯAOC=ЁЯBODЃЌ
ЭЌРэПЩжЄЁЯOBD=ЁЯOACЃЌ
дкЁїAOCКЭЁїBODжаЃЌ
Ёп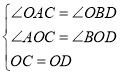 ЃЌ
ЃЌ
ЁрЁїAOCЁеЁїBODЃЈAASЃЉЃЌ
ЁрOA=OBЃЛ
ЃЈ2ЃЉШчЭМ1ЃЌЙ§ЕуAзїANЁЮODЃЌНЛOMбгГЄЯпгкЕуNЃЌ
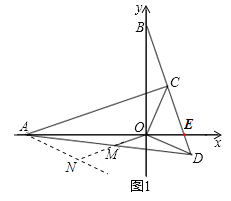
дђЁЯOAN+ЁЯAOD=180ЁуЃЌ
ЁпЁЯAOB=ЁЯCOD=90ЁуЃЌ
ЁрЁЯAOD+ЁЯBOC=180ЁуЃЌ
ЁрЁЯOAN=ЁЯBOCЃЌ
гжЁпOMЁЮACЃЌ
ЁрЁЯAON=ЁЯCAOЃЌ
гЩЃЈ1ЃЉжЊЁЯCAO=ЁЯOBCЃЌ
ЁрЁЯAON=ЁЯOBCЃЌ
гжЁпOA=OBЃЌ
ЁрЁїBOCЁеЁїOANЃЈASAЃЉЃЌ
ЁрBC=ONЃЌAN=OC=ODЃЌ
ЁпANЁЮODЃЌ
ЁрЁЯMAN=ЁЯMDOЃЌЁЯMNA=ЁЯMODЃЌ
ЁрЁїAMNЁеЁїDMOЃЈASAЃЉЃЌ
ЁрOM=MN=![]() ONЃЌМДON=2OMЃЌ
ONЃЌМДON=2OMЃЌ
ЁрBC=2OMЃЛ
ЃЈ3ЃЉШчЭМ2ЃЌЙ§ЕуFзїFTЁЭDGЃЌНЛDGбгГЄЯпгкЕуTЃЌ
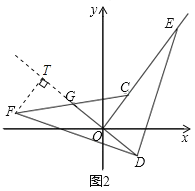
дђЁЯFTD=ЁЯDOE=90ЁуЃЌ
ЁрЁЯODE+ЁЯOED=90ЁуЃЌ
гжЁпDEЁЭDFЃЌ
ЁрЁЯODE+ЁЯFDT=90ЁуЃЌ
ЁрЁЯOED=ЁЯTDFЃЌ
ЁпDE=DFЃЌ
ЁрЁїFTDЁеЁїDOEЃЈAASЃЉЃЌ
ЁрFT=ODЃЌDT=OEЃЌ
ЁпOD=OCЃЌ
ЁрFT=OCЃЌ
ЁпЁЯFTG=ЁЯCOG=90ЁуЃЌЁЯFGT=ЁЯCGOЃЌ
ЁрЁїFTGЁеЁїCOGЃЈAASЃЉЃЌ
ЁрOT=2OG=8ЃЌ
ЁпOE=DTЃЌOC=ODЃЌ
ЁрCE=OT=8ЃЎ


 ЖсЙкбЕСЗЕЅдЊЦкФЉГхДЬ100ЗжЯЕСаД№АИ
ЖсЙкбЕСЗЕЅдЊЦкФЉГхДЬ100ЗжЯЕСаД№АИ аТЫМЮЌаЁЙкОќ100ЗжзївЕБОЯЕСаД№АИ
аТЫМЮЌаЁЙкОќ100ЗжзївЕБОЯЕСаД№АИ УћЪІжИЕМвЛОэЭЈЯЕСаД№АИ
УћЪІжИЕМвЛОэЭЈЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЪЧЖўДЮКЏЪ§yЃН![]() ЃЋbxЃЋcЭМЯёЕФвЛВПЗжЃЌЭМЯёЙ§ЕуAЃЈЃ3ЃЌ0ЃЉЃЌЖдГЦжсЪЧжБЯпxЃНЃ1ЃЌИјГіЫФИіНсТлЃЌЦфжае§ШЗНсТлЕФИіЪ§ЮЊЃЈ ЃЉ
ЃЋbxЃЋcЭМЯёЕФвЛВПЗжЃЌЭМЯёЙ§ЕуAЃЈЃ3ЃЌ0ЃЉЃЌЖдГЦжсЪЧжБЯпxЃНЃ1ЃЌИјГіЫФИіНсТлЃЌЦфжае§ШЗНсТлЕФИіЪ§ЮЊЃЈ ЃЉ
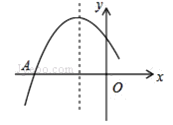
ЂйcЃО0ЃЛ Ђк 2aЃbЃН0ЃЛ Ђл![]() ЃМ0. ЂмШєЕуBЃЈЃ
ЃМ0. ЂмШєЕуBЃЈЃ![]() ЃЌ
ЃЌ![]() ЃЉЁЂCЃЈЃ
ЃЉЁЂCЃЈЃ![]() ЃЌ
ЃЌ![]() ЃЉдкЭМЯёЩЯЃЌдђ
ЃЉдкЭМЯёЩЯЃЌдђ![]() ЃМ
ЃМ![]()
A. 1 B. 2 C. 3 D. 4
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
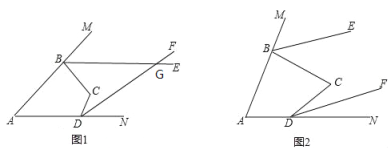
ЁОЬтФПЁПШчЭМЃЌЫФБпаЮABCDЃЌBEЁЂDFЗжБ№ЦНЗжЫФБпаЮЕФЭтНЧЁЯMBCКЭЁЯNDCЃЌШєЁЯBAD=ІСЃЌЁЯBCD=ІТ
ЃЈ1ЃЉШчЭМЃЌШєІС+ІТ=120ЁуЃЌЧѓЁЯMBC+ЁЯNDCЕФЖШЪ§ЃЛ
ЃЈ2ЃЉШчЭМЃЌШєBEгыDFЯрНЛгкЕуGЃЌЁЯBGD=30ЁуЃЌЧыаДГіІСЁЂІТЫљТњзуЕФЕШСПЙиЯЕЪНЃЛ
ЃЈ3ЃЉШчЭМЃЌШєІС=ІТЃЌХаЖЯBEЁЂDFЕФЮЛжУЙиЯЕЃЌВЂЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПаЁбЇЪБКђДѓМвЯВЛЖЭцЕФЛУЗНгЮЯЗЃЌРЯЪІЩдМгДДаТИФГЩСЫЁАЛУдВЁБгЮЯЗЃЌЯждкНЋЉ1ЁЂ2ЁЂЉ3ЁЂ4ЁЂЉ5ЁЂ6ЁЂЉ7ЁЂ8ЗжБ№ЬюШыЭМжаЕФдВШІФкЃЌЪЙКсЁЂЪњвдМАФкЭтСНШІЩЯЕФ4ИіЪ§зжжЎКЭЖМЯрЕШЃЌРЯЪІвбОАяжњЭЌбЇУЧЭъГЩСЫВПЗжЬюПеЃЌдђЭМжаa+bЕФжЕЮЊЃЈЁЁЁЁЃЉ

A. Љ6ЛђЉ3 B. Љ8Лђ1 C. Љ1ЛђЉ4 D. 1ЛђЉ1
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЗНИёжНжаУПИіаЁе§ЗНаЮЕФБпГЄЖМЮЊ1ЃЌдкЗНИёжНФкНЋ![]() ОЙ§вЛДЮЦНвЦКѓЕУЕН
ОЙ§вЛДЮЦНвЦКѓЕУЕН![]() ЃЌЭМжаБъГіСЫЕу
ЃЌЭМжаБъГіСЫЕу![]() ЕФЖдгІЕу
ЕФЖдгІЕу![]() ЃЌРћгУЭјИёЕуКЭШ§НЧАхЛЭМЛђМЦЫуЃК
ЃЌРћгУЭјИёЕуКЭШ§НЧАхЛЭМЛђМЦЫуЃК

ЃЈ1ЃЉдкИјЖЈЗНИёжНжаЛГіЦНвЦКѓЕФ![]() ЃЎ
ЃЎ
ЃЈ2ЃЉЛГі![]() БпЕФжаЯп
БпЕФжаЯп![]() ЃЎ
ЃЎ
ЃЈ3ЃЉЛГі![]() БпЕФИпЯп
БпЕФИпЯп![]() ЃЎ
ЃЎ
ЃЈ4ЃЉ![]() ЕФУцЛ§ЮЊ ЃЎ
ЕФУцЛ§ЮЊ ЃЎ
ЃЈ5ЃЉдкЭМжаФмЪЙ![]() ЕФИёЕу
ЕФИёЕу![]() ЕФИіЪ§га Иі ЃЈЕу
ЕФИіЪ§га Иі ЃЈЕу![]() вьгкЕу
вьгкЕу![]() ЃЉЃЎ
ЃЉЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПаТЖЈвхЃКЖдЗЧИКЪ§ЁАЫФЩсЮхШыЁБЕНИіЮЛЕФжЕМЧЮЊ![]() ЃЌМДЕБ
ЃЌМДЕБ![]() ЮЊЗЧИКећЪ§ЪБЃЌШє
ЮЊЗЧИКећЪ§ЪБЃЌШє![]() ЃЌдђ
ЃЌдђ![]() ШчЃК
ШчЃК![]() ЃЌЪдНтОіЯТСаЮЪЬт
ЃЌЪдНтОіЯТСаЮЪЬт
ЃЈ1ЃЉЬюПеЃКЂй![]() ЂкШє
ЂкШє![]() ЃЌдђЪЕЪ§
ЃЌдђЪЕЪ§![]() ЕФШЁжЕЗЖЮЇЮЊ
ЕФШЁжЕЗЖЮЇЮЊ
ЃЈ2ЃЉдкЙигк![]() ЕФЗНГЬзщ
ЕФЗНГЬзщ![]() жаЃЌШєЮДжЊЪ§
жаЃЌШєЮДжЊЪ§![]() Тњзу
Тњзу![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФжЕЃЎ
ЕФжЕЃЎ
ЃЈ3ЃЉЕБ![]() ЪБЃЌШє
ЪБЃЌШє![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФзюаЁжЕЃЎ
ЕФзюаЁжЕЃЎ
ЃЈ4ЃЉЧѓТњзу![]() ЕФЫљгаЗЧИКЪЕЪ§
ЕФЫљгаЗЧИКЪЕЪ§![]() ЕФжЕЃЌЧыжБНгаДГіД№АИ ЃЎ
ЕФжЕЃЌЧыжБНгаДГіД№АИ ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЩфбєЯиЪЕбщГѕжаЮЊСЫНтШЋаЃбЇЩњЩЯбЇЦкВЮМгЩчЧјЛюЖЏЕФЧщПіЃЌбЇаЃЫцЛњЕїВщСЫБОаЃ50УћбЇЩњВЮМгЩчЧјЛюЖЏЕФДЮЪ§ЃЌВЂНЋЕїВщЫљЕУЕФЪ§ОнећРэШчЯТЃК
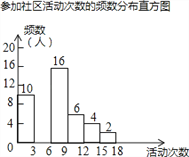
ВЮМгЩчЧјЛюЖЏДЮЪ§ЕФЦЕЪ§ЁЂЦЕТЪЗжВМБэ
ЛюЖЏДЮЪ§x | ЦЕЪ§ | ЦЕТЪ |
0ЃМxЁм3 | 10 | 0.20 |
3ЃМxЁм6 | a | 0.24 |
6ЃМxЁм9 | 16 | 0.32 |
9ЃМxЁм12 | 6 | 0.12 |
12ЃМxЁм15 | m | b |
15ЃМxЁм18 | 2 | n |
ИљОнвдЩЯЭМБэаХЯЂЃЌНтД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉБэжаa=ЁЁЁЁЃЌb=ЁЁЁЁЃЛ
ЃЈ2ЃЉЧыАбЦЕЪ§ЗжВМжБЗНЭМВЙГфЭъећЃЈЛЭМКѓЧыБъзЂЯргІЕФЪ§ОнЃЉЃЛ
ЃЈ3ЃЉШєИУаЃЙВга1200УћбЇЩњЃЌЧыЙРМЦИУаЃдкЩЯбЇЦкВЮМгЩчЧјЛюЖЏГЌЙ§6ДЮЕФбЇЩњгаЖрЩйШЫЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮвУЧжЊЕРЃЌШЮвтвЛИіе§ећЪ§nЖМПЩвдНјааетбљЕФЗжНтЃКn=pЁСqЃЈpЃЌqЪЧе§ећЪ§ЃЌЧвpЁмqЃЉЃЌдкnЕФЫљгаетжжЗжНтжаЃЌШчЙћpЃЌqСНвђЪ§жЎВюЕФОјЖджЕзюаЁЃЌЮвУЧОЭГЦpЁСqЪЧnЕФзюМбЗжНтЃЌВЂЙцЖЈЃКFЃЈnЃЉ=![]() ЃЌР§Шч12ПЩвдЗжНтГЩ1ЁС12,2ЁС6Лђ3ЁС4ЃЌвђЮЊ12-1ЃО6-2ЃО4-3ЃЌЫљга3ЁС4ЪЧзюМбЗжНтЃЌЫљвдFЃЈ12ЃЉ=
ЃЌР§Шч12ПЩвдЗжНтГЩ1ЁС12,2ЁС6Лђ3ЁС4ЃЌвђЮЊ12-1ЃО6-2ЃО4-3ЃЌЫљга3ЁС4ЪЧзюМбЗжНтЃЌЫљвдFЃЈ12ЃЉ=![]() .
.
ЃЈ1ЃЉШчЙћвЛИіе§ећЪ§aЪЧСэЭтвЛИіе§ећЪ§bЕФЦНЗНЃЌЮвУЧГЦе§ећЪ§aЪЧЭъШЋЦНЗНЪ§ЃЌЧѓжЄЃКЖдШЮвтвЛИіЭъШЋЦНЗНЪ§mЃЌзмгаFЃЈmЃЉ=1.
ЃЈ2ЃЉШчЙћвЛИіСНЮЛе§ећЪ§tЃЌt=10x+yЃЈ1ЁмxЁмyЁм9,x,yЮЊздШЛЪ§ЃЉЃЌНЛЛЛЦфИіЮЛЩЯЕФЪ§гыЪЎЮЛЩЯЕФЪ§ЕУЕНЕФаТЪ§МѕШЅдРДЕФСНЮЛе§ећЪ§ЫљЕУЕФВюЮЊ18ЃЌФЧУДЮвУЧГЦетИіЪ§tЮЊЁАМЊЯщЪ§ЁБЃЌЧѓЫљгаЁАМЊЯщЪ§ЁБжаFЃЈtЃЉЕФзюДѓжЕ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЫФБпаЮABCDжаЁЯADC=ЁЯABC=90ЁуЃЌAD=CDЃЌDPЁЭABгкЕуPЃЌШєЫФБпаЮABCDЕФУцЛ§ЪЧ9ЃЌдђDPЕФГЄЪЧ________.

ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com