
ЁОЬтФПЁПШчЭМЃЌвбжЊжБЯп![]() НЛxжсЁЂyжсЗжБ№гкЕуAЁЂЕуFЃЌВЂгыЗДБШР§КЏЪ§
НЛxжсЁЂyжсЗжБ№гкЕуAЁЂЕуFЃЌВЂгыЗДБШР§КЏЪ§![]() ЕФЭМЯёНЛгкBЁЂCСНЕуЃЈЕуBдкЕуCЕФзѓВрЃЉЃЌвдOAЮЊжБОЖзїАыдВЃЌдВаФЮЊPЃЌЙ§ЕуBзїxжсЕФДЙЯпЃЌДЙзуЮЊEЃЌВЂгыАыдВPНЛгкЕуDЃЎ
ЕФЭМЯёНЛгкBЁЂCСНЕуЃЈЕуBдкЕуCЕФзѓВрЃЉЃЌвдOAЮЊжБОЖзїАыдВЃЌдВаФЮЊPЃЌЙ§ЕуBзїxжсЕФДЙЯпЃЌДЙзуЮЊEЃЌВЂгыАыдВPНЛгкЕуDЃЎ
ЃЈ1ЃЉШєBЁЂCЕФКсзјБъЗжБ№ЮЊx1ЁЂx2ЃЌЧвx2x15ЃЌЧѓmЕФжЕЃЛ
ЃЈ2ЃЉХаЖЯЯпЖЮDEЕФГЄЪЧЗёЫцmЕФИФБфЖјИФБфЃЌШєВЛЫцmЕФИФБфЖјИФБфЃЌЧыЧѓГіDEЕФГЄЃЛШєЫцmЕФИФБфЖјИФБфЃЌЧыЫЕУїРэгЩЃЛ
ЃЈ3ЃЉМЧЕуCЙигкжБЯпDEЕФЖдГЦЕуЮЊCЁфЃЌЕБЫФБпаЮCDCЁфEЮЊСтаЮЪБЃЌжБНгаДГіCЕФзјБъКЭmЕФжЕЃЎ

ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЛЃЈ2ЃЉВЛИФБфЃЌ
ЃЛЃЈ2ЃЉВЛИФБфЃЌ![]() ЃЛЃЈ3ЃЉ
ЃЛЃЈ3ЃЉ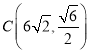 ЃЌ
ЃЌ![]()
ЁОНтЮіЁП
ЃЈ1ЃЉЩш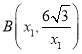 ЃЌ
ЃЌ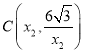 ЃЌИљОнЕуBЃЌЕуCдквЛДЮКЏЪ§гыЗДБШР§КЏЪ§ЕФЭМЯѓЩЯЃЌСаГіЗНГЬзщЃЌЧѓНтМДПЩЃЛ
ЃЌИљОнЕуBЃЌЕуCдквЛДЮКЏЪ§гыЗДБШР§КЏЪ§ЕФЭМЯѓЩЯЃЌСаГіЗНГЬзщЃЌЧѓНтМДПЩЃЛ
ЃЈ2ЃЉСЌНг![]() ЁЂ
ЁЂ![]() ЃЌИљОн
ЃЌИљОн![]() ЕУГі
ЕУГі![]() ЃЌЩш
ЃЌЩш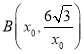 ЃЌ
ЃЌ![]() ЃЌЭЈЙ§МЦЫуЕУГі
ЃЌЭЈЙ§МЦЫуЕУГі![]() ЃЌ
ЃЌ![]() ЃЌДњШыЧѓНтМДПЩЃЛ
ЃЌДњШыЧѓНтМДПЩЃЛ
ЃЈ3ЃЉСЌНгCCЁфЃЌЩшDEгыCCЁфНЛгкGЃЌгЩЃЈ2ЃЉгыСтаЮЕФаджЪЕУГіDGЃНEGЃН![]() ЃЌНјЖјЕУГіЕуCЕФзнзјБъЃЌЧѓНтМДПЩЃЎ
ЃЌНјЖјЕУГіЕуCЕФзнзјБъЃЌЧѓНтМДПЩЃЎ
НтЃКЃЈ1ЃЉгЩЬтвтЕУЃЌ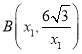 ЃЌ
ЃЌ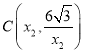
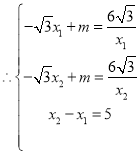 ЃЌ
ЃЌ
ЯћШЅ![]() ЕУЃЌ
ЕУЃЌ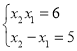 ЃЌ
ЃЌ
НтЕУЃЌ![]() ЃЈЩсШЅЃЉЛђ1ЃЌ
ЃЈЩсШЅЃЉЛђ1ЃЌ![]() ЃЌ
ЃЌ
ЁрЕУ![]() ЃЌДњШы
ЃЌДњШы![]() ЕУЃЌ
ЕУЃЌ![]() ЃЛ
ЃЛ
ЃЈ2ЃЉСЌНг![]() ЁЂ
ЁЂ![]() ЃЌвзжЄ
ЃЌвзжЄ![]() ЃЌ
ЃЌ
Ёр![]() МД
МД![]() ЃЌ
ЃЌ
Щш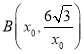 ЃЌдђ
ЃЌдђ ЃЌМД
ЃЌМД![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
ЁрDEЕФГЄВЛИФБфЃЌЮЊ![]() ЃЛ
ЃЛ
ЃЈ3ЃЉСЌНгCCЁфЃЌЩшDEгыCCЁфНЛгкGЃЌ
гЩЃЈ2ЃЉЕУЃЌ![]() ЃЌ
ЃЌ
ЁпЫФБпаЮCDCЁфEЮЊСтаЮЃЌ
ЁрDGЃНEGЃН![]() ЃЌ
ЃЌ
ЁрCЕФзнзјБъЮЊ![]() ЃЌ
ЃЌ
ЕБyЃН![]() ЪБЃЌ
ЪБЃЌ![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр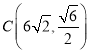 ЃЌ
ЃЌ
НЋЕу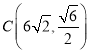 ДњШы
ДњШы![]() жаЕУЃК
жаЕУЃК![]() ЃЌ
ЃЌ
Ёр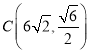 ЃЌ
ЃЌ![]() ЃЎ
ЃЎ




| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
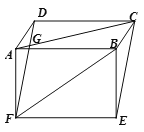
ЁОЬтФПЁПвбжЊЃКШчЭМЃЌдкЦНааЫФБпаЮABCDКЭОиаЮABEFжаЃЌACгыDFЯрНЛгкЕуG.
(1) ЪдЫЕУїDFЃНCEЃЛ
(2) ШєACЃНBFЃНDFЃЌЧѓЁЯACEЕФЖШЪ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
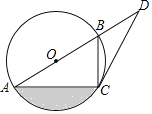
ЁОЬтФПЁПШчЭМЃЌвбжЊABЪЧЁбOЩЯЕФЕуЃЌCЪЧЁбOЩЯЕФЕуЃЌЕуDдкABЕФбгГЄЯпЩЯЃЌЁЯBCD=ЁЯBACЃЎ
ЃЈ1ЃЉЧѓжЄЃКCDЪЧЁбOЕФЧаЯпЃЛ
ЃЈ2ЃЉШєЁЯD=30ЁуЃЌBD=2ЃЌЧѓЭМжавѕгАВПЗжЕФУцЛ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
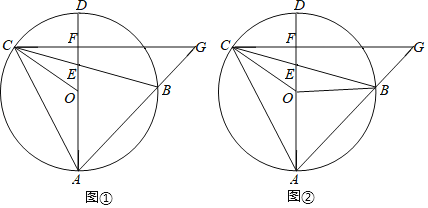
ЁОЬтФПЁПШчЭМЂйЃЌвбжЊЁїABCФкНггкЁбOЃЌBCНЛжБОЖADгкЕуEЃЌЙ§ЕуCзїADЕФДЙЯпНЛABЕФбгГЄЯпгкЕуGЃЌДЙзуЮЊFЃЌСЌНгOCЃЎ
ЃЈ1ЃЉЧѓжЄЃКЁЯACBЃНЁЯGЃЛ
ЃЈ2ЃЉШчЭМЂкЃЌСЌНгOBЃЌШєABЃНAEЃЌ![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФжЕЃЎ
ЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЕуA(0ЃЌ3)ЃЌ![]() ЃЌЙ§ЕуAзїABЕФДЙЯпНЛxжсгкЕуA1ЃЌЙ§A1зїAA1ЕФДЙЯпНЛyжсгкЕуA2ЃЌЙ§ЕуA2зїA1A2ЕФДЙЯпНЛxжсгкЕуA3ЁЁЃЌАДДЫЙцТЩМЬајзїЯТШЅЃЌжБжСЕУЕНЕуA2018ЮЊжЙЃЌдђЕуA2018зјБъЮЊ__________ЃЎ
ЃЌЙ§ЕуAзїABЕФДЙЯпНЛxжсгкЕуA1ЃЌЙ§A1зїAA1ЕФДЙЯпНЛyжсгкЕуA2ЃЌЙ§ЕуA2зїA1A2ЕФДЙЯпНЛxжсгкЕуA3ЁЁЃЌАДДЫЙцТЩМЬајзїЯТШЅЃЌжБжСЕУЕНЕуA2018ЮЊжЙЃЌдђЕуA2018зјБъЮЊ__________ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
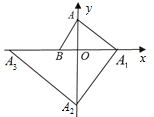
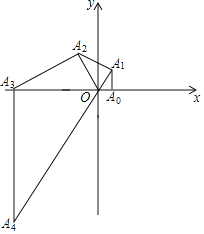
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕФкЃЌЁЯOA0A1ЃН90ЁуЃЌЁЯA1OA0ЃН60ЁуЃЌвдOA1ЮЊжБНЧБпЯђЭтзїRtЁїOA1A2ЃЌЪЙЁЯA2A1OЃН90ЁуЃЌЁЯA2OA1ЃН60ЁуЃЌАДДЫЗНЗЈНјааЯТШЅЃЌЕУЕН RtЁїOA2A3ЃЌRtЁїOA3A4ЁЃЌШєЕуA0ЕФзјБъЪЧЃЈ1ЃЌ0ЃЉЃЌдђЕуA13ЕФКсзјБъЪЧ_____ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкRtЁїABCжаЃЌЁЯABCЃН90ЁуЃЌвдABЮЊжБОЖзїАыдВЁбOНЛACгкЕуDЃЌЕуEЮЊBCЕФжаЕуЃЌСЌНгDE.

(1)ЧѓжЄЃКDEЪЧАыдВЁбOЕФЧаЯпЃЛ
(2)ШєЁЯBACЃН30ЁуЃЌDEЃН2ЃЌЧѓADЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
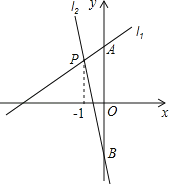
ЁОЬтФПЁПШчЭМЃЌжБЯпl1гыl2ЯрНЛгкЕуPЃЌЕуPКсзјБъЮЊЉ1ЃЌl1ЕФНтЮіЪНЮЊyЃН![]() x+3ЃЌЧвl1гыyжсНЛгкЕуAЃЌl2гыyжсНЛгкЕуBЃЌЕуAгыЕуBЧЁКУЙигкxжсЖдГЦЃЎ
x+3ЃЌЧвl1гыyжсНЛгкЕуAЃЌl2гыyжсНЛгкЕуBЃЌЕуAгыЕуBЧЁКУЙигкxжсЖдГЦЃЎ
ЃЈ1ЃЉЧѓЕуBЕФзјБъЃЛ
ЃЈ2ЃЉЧѓжБЯпl2ЕФНтЮіЪНЃЛ
ЃЈ3ЃЉШєЕуMЮЊжБЯпl2ЩЯвЛЖЏЕуЃЌжБНгаДГіЪЙЁїMABЕФУцЛ§ЪЧЁїPABЕФУцЛ§ЕФ![]() ЕФЕуMЕФзјБъЃЛ
ЕФЕуMЕФзјБъЃЛ
ЃЈ4ЃЉЕБxЮЊКЮжЕЪБЃЌl1ЃЌl2БэЪОЕФСНИіКЏЪ§ЕФКЏЪ§жЕЖМДѓгк0ЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
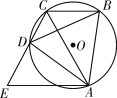
ЁОЬтФПЁПШчЭМЃЌЫФБпаЮABCDФкНггкЁбOЃЌACгыBDЮЊЖдНЧЯпЃЌЁЯBCAЃНЁЯBADЃЌЙ§ЕуAзїAEЁЮBCНЛCDЕФбгГЄЯпгкЕуEЃЎ
(1)ЧѓжЄЃКECЃНACЃЛ
(2)ШєcosЁЯADBЃН![]() ЃЌBCЃН10ЃЌЧѓDEЕФГЄЃЎ
ЃЌBCЃН10ЃЌЧѓDEЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com