
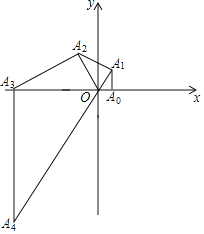
【题目】如图,在平面直角坐标系内,∠OA0A1=90°,∠A1OA0=60°,以OA1为直角边向外作Rt△OA1A2,使∠A2A1O=90°,∠A2OA1=60°,按此方法进行下去,得到 Rt△OA2A3,Rt△OA3A4…,若点A0的坐标是(1,0),则点A13的横坐标是_____.
【答案】212.
【解析】
根据![]() ,
,![]() ,点
,点![]() 的坐标是
的坐标是![]() ,得
,得![]() ,点
,点![]() 的横坐标是
的横坐标是![]() ,点
,点![]() 的横坐标是-
的横坐标是-![]() ,同理可得点
,同理可得点![]() 的横坐标是
的横坐标是![]() ,点
,点![]() 的横坐标是
的横坐标是![]() ,点
,点![]() 的横坐标是
的横坐标是![]() ,点
,点![]() 的横坐标是
的横坐标是![]() ,点
,点![]() 的横坐标是
的横坐标是![]() ,依次进行下去,可得点
,依次进行下去,可得点![]() 的横坐标.
的横坐标.
解:∵∠OA0A1=90°,∠A1OA0=60°,点A0的坐标是(1,0),
∴OA0=1,
∴点A1 的横坐标是 1=20,
∴OA1=2OA0=2,
∵∠A2A1O=90°,∠A2OA1=60°,
∴OA2=2OA1=4,
∴点A2 的横坐标是- ![]() OA2=-2=-21,
OA2=-2=-21,
依次进行下去,Rt△OA2A3,Rt△OA3A4…,
同理可得:
点A3 的横坐标是﹣2OA2=﹣8=﹣23,
点A4 的横坐标是﹣8=﹣23,
点A5 的横坐标是 ![]() OA5=
OA5=![]() ×2OA4=2OA3=4OA2=16=24,
×2OA4=2OA3=4OA2=16=24,
点A6 的横坐标是2OA5=2×2OA4=23OA3=64=26,
点A7 的横坐标是64=26,
…
发现规律,
点A12 的横坐标是212,
则点A13的横坐标是 212.
故答案为:212.


 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案科目:初中数学 来源: 题型:
【题目】已知:如图,一次函数y=-2x与二次函数y=ax2+2ax+c的图像交于A、B两点(点A在点B的右侧),与其对称轴交于点C.
(1)求点C的坐标;
(2)设二次函数图像的顶点为D,点C与点D关于 x轴对称,且△ACD的面积等于2.
① 求二次函数的解析式;
② 在该二次函数图像的对称轴上求一点P(写出其坐标),使△PBC与△ACD相似.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() :
:![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,其对称轴
,其对称轴![]() 与
与![]() 轴交于点
轴交于点![]() .
.

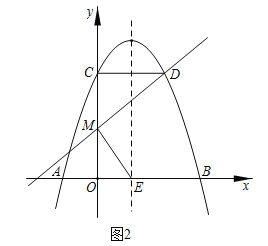
(1)求抛物线![]() 的表达式;
的表达式;
(2)如图1,若动点![]() 在对称轴
在对称轴![]() 上,当
上,当![]() 的周长最小时,求点
的周长最小时,求点![]() 的坐标;
的坐标;
(3)如图2,设点![]() 关于对称轴
关于对称轴![]() 的对称点为
的对称点为![]() ,
,![]() 是线段
是线段![]() 上的一个动点,若
上的一个动点,若![]() ,求直线
,求直线![]() 的表达式.
的表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
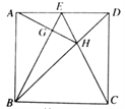
【题目】如图,正方形ABCD的边长为6,点E是AD的中点,连接BE、CE,CE与BD相交于点H,连接AH,交BE于点G,则GH的长为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线![]() 交x轴、y轴分别于点A、点F,并与反比例函数
交x轴、y轴分别于点A、点F,并与反比例函数![]() 的图像交于B、C两点(点B在点C的左侧),以OA为直径作半圆,圆心为P,过点B作x轴的垂线,垂足为E,并与半圆P交于点D.
的图像交于B、C两点(点B在点C的左侧),以OA为直径作半圆,圆心为P,过点B作x轴的垂线,垂足为E,并与半圆P交于点D.
(1)若B、C的横坐标分别为x1、x2,且x2x15,求m的值;
(2)判断线段DE的长是否随m的改变而改变,若不随m的改变而改变,请求出DE的长;若随m的改变而改变,请说明理由;
(3)记点C关于直线DE的对称点为C′,当四边形CDC′E为菱形时,直接写出C的坐标和m的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
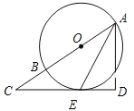
【题目】如图,AB是⊙O的直径,过点E作⊙O的切线ED,AD⊥ED于D,直线ED交AB的延长线于点C.
(1)求证:AE平分∠CAD.
(2)若BC=2,CE=4,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“低碳生活,绿色出行”是我们倡导的一种生活方式,有关部门抽样调查了某单位员工上下班的交通方式,绘制了两幅统计图:
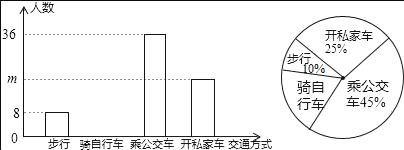
(1)样本中的总人数为 人;扇形统计十图中“骑自行车”所在扇形的圆心角为 度;
(2)补全条形统计图;
(3)该单位共有1000人,积极践行这种生活方式,越来越多的人上下班由开私家车改为骑自行车.若步行,坐公交车上下班的人数保持不变,问原来开私家车的人中至少有多少人改为骑自行车,才能使骑自行车的人数不低于开私家车的人数?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:解方程x2﹣|x|﹣2=0解:(1)当x≥0时,原方程可以化为x2﹣x﹣2=0,
解得x1=2,x2=﹣1<0(不合题意,舍去);(2)当x<0时,原方程可以化为x2+x﹣2=0,解得x1=﹣2,x2=1>0(舍去).∴原方程的解为x1=2,x2=﹣2.那么方程x2﹣|x﹣1|﹣1=0的解为( )
A.![]() =0,
=0,![]() =1B.
=1B.![]() =﹣2,
=﹣2,![]() =1
=1
C.![]() =1,
=1,![]() =﹣2D.
=﹣2D.![]() =1,
=1,![]() =2
=2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】老师随机抽查了本学期学生读课外书册数的情况,绘制成条形图(图1)和不完整的扇形图(图2),其中条形图被墨迹遮盖了一部分.
(1)求条形图中被遮盖的数,并写出册数的中位数;
(2)在所抽查的学生中随机选一人谈读书感想,求选中读书超过5册的学生的概率;
(3)随后又补查了另外几人,得知最少的读了6册,将其与之前的数据合并后,发现册数的中位数没改变,则最多补查了 人.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com