
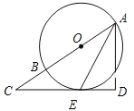
【题目】如图,AB是⊙O的直径,过点E作⊙O的切线ED,AD⊥ED于D,直线ED交AB的延长线于点C.
(1)求证:AE平分∠CAD.
(2)若BC=2,CE=4,求⊙O的半径.
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
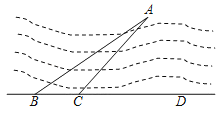
【题目】如图,为测量小岛A到公路BD的距离,先在点B处测得∠ABD=37°,再沿BD方向前进150m到达点C,测得∠ACD=45°,求小岛A到公路BD的距离.(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】长沙市为推进养老服务工作的深入开展,在科学规划养老服务布局等方面作了大量工作,该市的养老机构拥有的养老床位数从2016年底的2万个增长到2018年底的2.42万个.
(1)求该市这两年养老床位数的年平均增长率;
(2)该市青竹湖社区养老中心拟建造三类养老专用房间(提供一个床位的单人间、提供两个床位的双人间、提供三个床位的三人间)共100间,设单人间有![]() 间(
间(![]() ),双人间的数量是单人间的2倍,且三人间的数量不少于单人间和双人间的数量之和,求此100间房建成后至少可提供床位多少个?
),双人间的数量是单人间的2倍,且三人间的数量不少于单人间和双人间的数量之和,求此100间房建成后至少可提供床位多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
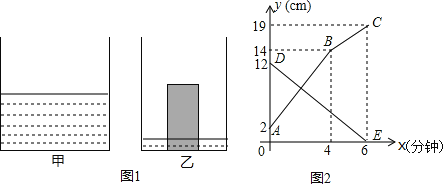
【题目】如图1是甲、乙两个圆柱形水槽的轴截面示意图,乙槽中有一圆柱形铁块放于其中(圆柱形铁块的下底面完全落在水槽底面上).现将甲槽中的水匀速注入乙槽,甲、乙两个水槽中水的深度y(厘米)与注水时间x(分钟)之间的关系如图2所示.根据图象提供的信息,解答下列问题:
(1)注水多长时间时,甲、乙两个水槽中的水的深度相同?
(2)若乙槽底面积为42平方厘米(壁厚不计),求乙槽中铁块的体积;
(3)若乙槽中铁块的体积为168立方厘米(壁厚不计),求甲槽底面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
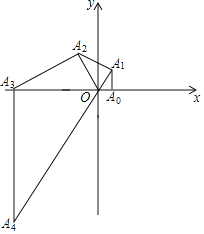
【题目】如图,在平面直角坐标系内,∠OA0A1=90°,∠A1OA0=60°,以OA1为直角边向外作Rt△OA1A2,使∠A2A1O=90°,∠A2OA1=60°,按此方法进行下去,得到 Rt△OA2A3,Rt△OA3A4…,若点A0的坐标是(1,0),则点A13的横坐标是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边![]() 的顶点
的顶点![]() ,
,![]() ,规定把
,规定把![]() “先沿
“先沿![]() 轴翻折,再向左平移1个单位”为一次变换,这样连续经过2019次变换后,等边
轴翻折,再向左平移1个单位”为一次变换,这样连续经过2019次变换后,等边![]() 的顶点
的顶点![]() 的坐标为( )
的坐标为( )
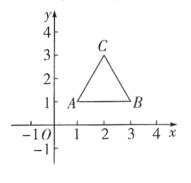
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
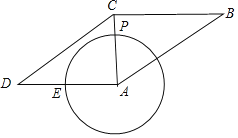
【题目】如图,已知P是半径为3的⊙A上一点,延长AP到点C,使AC=4,以AC为对角线作ABCD,AB=4![]() ,⊙A交边AD于点E,当ABCD面积为最大值时,
,⊙A交边AD于点E,当ABCD面积为最大值时,![]() 的长为( )
的长为( )
A.![]() πB.πC.
πB.πC.![]() πD.3π
πD.3π
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1是一个地铁站入口的双翼闸机.如图2,它的双翼展开时,双翼边缘的端点A与B之间的距离为10cm,双翼的边缘AC=BD=54cm,且与闸机侧立面夹角∠PCA=∠BDQ=30°.当双翼收起时,可以通过闸机的物体的最大宽度为( )

A. (54![]() +10) cm B. (54
+10) cm B. (54![]() +10) cm C. 64 cm D. 54cm
+10) cm C. 64 cm D. 54cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰△ABC中,AB=AC,∠A=36°,△ABC绕点B逆时针方向旋转一定角度后到△BDE的位置,点D落在边AC上
问:(1)旋转角是几度?为什么?
(2)将AB与DE的交点记为F,除△ABC和△BDE外,图中还有几个等腰三角形?写出图中所有的等腰三角形
(3)请选择题(2)中找到的一个等腰三角形说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com