
【题目】如图,等腰△ABC中,AB=AC,∠A=36°,△ABC绕点B逆时针方向旋转一定角度后到△BDE的位置,点D落在边AC上
问:(1)旋转角是几度?为什么?
(2)将AB与DE的交点记为F,除△ABC和△BDE外,图中还有几个等腰三角形?写出图中所有的等腰三角形
(3)请选择题(2)中找到的一个等腰三角形说明理由.

【答案】(1)36°,见解析;(2)5个,△BCD,△BDF,△BEF,△ADF,△ABD;(3)△BCD,见解析
【解析】
(1)根据旋转的性质,可得BD=BC,然后根据等腰三角形的性质即可求解;
(2)求得图形中的角的度数,根据等角对等边即可判断;
(3)根据等角对等边或旋转的性质判断.
解:(1)36°.
∵AB=AC,
∴∠ABC=∠C,
∵∠ABC+∠C+∠A=180°,∠A=36°,
∴∠ABC=∠C=72°.
∵BD=BC,
∴∠BDC=∠C=72°.
∴∠DBC=36°.
即旋转角为36°.
(2)图中还有5个等腰三角形,
分别是:△BCD,△BDF,△BEF,△ADF,△ABD;
(3)证:△BCD是等腰三角形.
证明:∵△ABC绕点B逆时针方向旋转一定角度后到△BDE的位置,
∴△ABC≌△BDE,
∴BD=DC,
即:△BCD是等腰三角形.


 一线名师权威作业本系列答案
一线名师权威作业本系列答案科目:初中数学 来源: 题型:
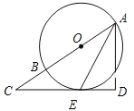
【题目】如图,AB是⊙O的直径,过点E作⊙O的切线ED,AD⊥ED于D,直线ED交AB的延长线于点C.
(1)求证:AE平分∠CAD.
(2)若BC=2,CE=4,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
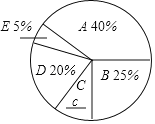
【题目】“全民阅读”活动,是中央宣传部、中央文明办和新闻出版总署贯彻落实关于建设学习型社会要求的一项重要举措.读书必须要讲究方法,只有按照一定的方法去阅读,才能取得事半功倍的效果.常用的阅读方法有:A.圈点批注法;B.摘记法;C.反思法:D.撰写读后感法;E.其他方法.某县某中学张老师为了解本校学生使用不同阅读方法读书的情况,随机抽取部分本校中学生进行了调查,通过数据的收集、整理绘制成以下不完整的统计图表,请根据图表中的信息解答下列问题:
中学生阅读方法情况统计表
阅读方法 | 频数 | |
A | 圈点批注法 | a |
B | 摘记法 | 20 |
C | 反思法 | b |
D | 撰写读后感法 | 16 |
E | 其他方法 | 4 |
(1)请你补全图表中的a,b,c数据:a= ,b= ,c= ;
(2)若该校共有中学生960名,估计该校使用“反思法”读书的学生有 人;
(3)小明从以上抽样调查所得结果估计全县6000名中学生中有1200人采用“撰写读后感法”读书,你同意小明的观点吗?请说明你的理由.
(4)该校决定从本次抽取的“其他方法”4名学生(记为甲,乙,丙,丁)中,随机选择2名成为学校阅读宣讲志愿者,请你用列表法或画树状图的方法,求恰好抽到甲和乙的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校九年级学生开展跳绳比赛活动,每班派5名学生参加,按团体总分多少排列名次,在规定时间内每人跳100个以上(含100个)为优秀.下表是甲班和乙班5名学生的比赛数据(每跳1个记1分,单位:分):
1号 | 2号 | 3号 | 4号 | 5号 | 总计 | |
甲班 | 100 | 98 | 110 | 89 | m | 500 |
乙班 | 89 | n | 95 | 119 | 97 | 500 |
经统计发现两班总分相等,此时有学生建议,可以通过考查数据中的其他信息作为参考,来确定冠军.请你回答下列问题:
(1)上表中,m=______,n=_____;
(2)若从两班参赛的这10名同学中,随机选择1人,求其成绩为优秀的概率;
(3)试从两班比赛成绩的优秀率、中位数和极差三个方面加以分析,判断冠军应该属于哪个班级?并简要说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】老师随机抽查了本学期学生读课外书册数的情况,绘制成条形图(图1)和不完整的扇形图(图2),其中条形图被墨迹遮盖了一部分.
(1)求条形图中被遮盖的数,并写出册数的中位数;
(2)在所抽查的学生中随机选一人谈读书感想,求选中读书超过5册的学生的概率;
(3)随后又补查了另外几人,得知最少的读了6册,将其与之前的数据合并后,发现册数的中位数没改变,则最多补查了 人.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有三张卡片(背面完全相同)分别写有![]() ,
,![]() ,
,![]() ,把它们背面朝上洗匀后,小军从中抽取一张,记下这个数后放回洗匀,小明又从中抽出一张.
,把它们背面朝上洗匀后,小军从中抽取一张,记下这个数后放回洗匀,小明又从中抽出一张.
![]() 两人抽取的卡片上的数是
两人抽取的卡片上的数是![]() 的概率是________.
的概率是________.
![]() 李刚为他们俩设定了一个游戏规则:若两人抽取的卡片上两数之积是有理数,则小军获胜,否则小明获胜,你认为这个游戏规则对谁有利?请用列表法或树状图进行分析说明.
李刚为他们俩设定了一个游戏规则:若两人抽取的卡片上两数之积是有理数,则小军获胜,否则小明获胜,你认为这个游戏规则对谁有利?请用列表法或树状图进行分析说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某汽车租赁公司对某款汽车的租赁方式按时段计费,该公司要求租赁方必须在9天内(包括9天)将所租汽车归还.租赁费用![]() (元)随时间
(元)随时间![]() (天)的变化图象为折线
(天)的变化图象为折线![]() ,如图所示.
,如图所示.
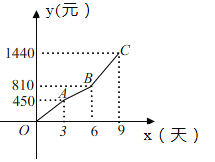
(1)当租赁时间不超过3天时,求每日租金.
(2)当![]() 时,求
时,求![]() (元)与
(元)与![]() (天)的函数关系式.
(天)的函数关系式.
(3)甲、乙两人租赁该款汽车各一辆,两人租赁的时间共为9天,甲租的天数少于3天,乙比甲多支付费用720元.请问乙租这款汽车多长时间?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(问题情境)
(1)古希腊著名数学家欧几里得在《几何原本》提出了射影定理,又称“欧几里德定理”:在直角三角形中,斜边上的高是两条直角边在斜边射影的比例中项,每一条直角边又是这条直角边在斜边上的射影和斜边的比例中项.射影定理是数学图形计算的重要定理.其符号语言是:如图1,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,则:(1)AC=AB·AD;(2)BC=AB·BD;(3)CD = AD·BD;请你证明定理中的结论(1)AC = AB·AD.
(结论运用)
(2)如图2,正方形ABCD的边长为3,点O是对角线AC、BD的交点,点E在CD上,过点C作CF⊥BE,垂足为F,连接OF,
①求证:△BOF∽△BED;
②若![]() ,求OF的长.
,求OF的长.
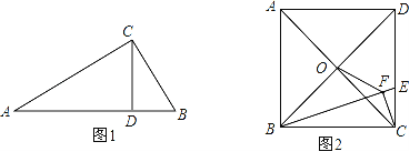
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探究
(1)如图①,在等腰直角三角形![]() 中,
中,![]() ,作
,作![]() 交
交![]() 于点
于点![]() ,点
,点![]() 为射线
为射线![]() 上一点,以点
上一点,以点![]() 为旋转中心将线段
为旋转中心将线段![]() 逆时针旋转90°得到线段
逆时针旋转90°得到线段![]() ,连接
,连接![]() 交射线
交射线![]() 于点
于点![]() ,连接
,连接![]() 、
、![]() .
.
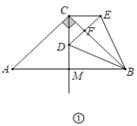
填空:
①线段![]() 、
、![]() 的数量关系为___________.
的数量关系为___________.
②线段![]() 、
、![]() 的位置关系为___________.
的位置关系为___________.
推广:
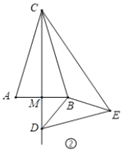
(2)如图②,在等腰三角形![]() 中,
中,![]() ,作
,作![]() 交
交![]() 于点
于点![]() ,点
,点![]() 为
为![]() 外部射线
外部射线![]() 上一点,以点
上一点,以点![]() 为旋转中心将线段
为旋转中心将线段![]() 逆时针旋转
逆时针旋转![]() 度得到线段
度得到线段![]() ,连接
,连接![]() 、
、![]() 、
、![]() 请判断(1)中的结论是否成立,并说明理由.
请判断(1)中的结论是否成立,并说明理由.
应用:
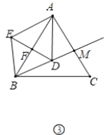
(3)如图③,在等边三角形![]() 中,
中,![]() .作
.作![]() 交
交![]() 于点
于点![]() ,点
,点![]() 为射线
为射线![]() 上一点,以点
上一点,以点![]() 为旋转中心将线段
为旋转中心将线段![]() 逆时针旋转60°得到线段
逆时针旋转60°得到线段![]() ,连接
,连接![]() 交射线
交射线![]() 于点
于点![]() ,连接
,连接![]() 、
、![]() .当以
.当以![]() 、
、![]() 、
、![]() 为顶点的三角形与
为顶点的三角形与![]() 全等时,请直接写出
全等时,请直接写出![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com