
【题目】探究
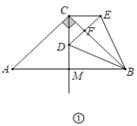
(1)如图①,在等腰直角三角形![]() 中,
中,![]() ,作
,作![]() 交
交![]() 于点
于点![]() ,点
,点![]() 为射线
为射线![]() 上一点,以点
上一点,以点![]() 为旋转中心将线段
为旋转中心将线段![]() 逆时针旋转90°得到线段
逆时针旋转90°得到线段![]() ,连接
,连接![]() 交射线
交射线![]() 于点
于点![]() ,连接
,连接![]() 、
、![]() .
.
填空:
①线段![]() 、
、![]() 的数量关系为___________.
的数量关系为___________.
②线段![]() 、
、![]() 的位置关系为___________.
的位置关系为___________.
推广:
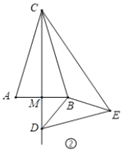
(2)如图②,在等腰三角形![]() 中,
中,![]() ,作
,作![]() 交
交![]() 于点
于点![]() ,点
,点![]() 为
为![]() 外部射线
外部射线![]() 上一点,以点
上一点,以点![]() 为旋转中心将线段
为旋转中心将线段![]() 逆时针旋转
逆时针旋转![]() 度得到线段
度得到线段![]() ,连接
,连接![]() 、
、![]() 、
、![]() 请判断(1)中的结论是否成立,并说明理由.
请判断(1)中的结论是否成立,并说明理由.
应用:
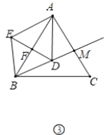
(3)如图③,在等边三角形![]() 中,
中,![]() .作
.作![]() 交
交![]() 于点
于点![]() ,点
,点![]() 为射线
为射线![]() 上一点,以点
上一点,以点![]() 为旋转中心将线段
为旋转中心将线段![]() 逆时针旋转60°得到线段
逆时针旋转60°得到线段![]() ,连接
,连接![]() 交射线
交射线![]() 于点
于点![]() ,连接
,连接![]() 、
、![]() .当以
.当以![]() 、
、![]() 、
、![]() 为顶点的三角形与
为顶点的三角形与![]() 全等时,请直接写出
全等时,请直接写出![]() 的值.
的值.
【答案】(1) BD=BE, BC⊥DE;(2) 结论:(1)中的结论仍然成立,理由见解析;(3)![]() 或
或![]() 或4.
或4.
【解析】
(1)如图①中,只要证明△CBD≌△CBE(SAS),再运用全等三角形的性质即可;
(2)结论不变。如图②中,只要证明△CBD≌△CBE(SAS),再运用全等三角形的性质即可;
(3)分点D在线段BM上和点D在线段BM的延长线上两种情形分别求解即可.
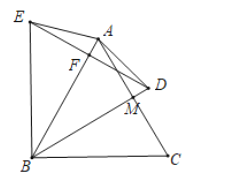
解:(1)如图①,
∵CA=CB,∠ACB=90°,CM平分∠ACB,
∴∠ACM=∠BCM=45°,
∵∠ECD=90°,
∴∠ECF=∠DCF=45°, CD=CE CB=CB
∴△CBD≌△CBE(SAS),
∴BD=BE,
∴CD=CE
∴BC垂直平分线段DE,
∴BC⊥DE.
故答案为BD=BE, BC⊥DE;
(2)结论:(1)中的结论仍然成立;理由:如图②,
∴CA=CB,∠ACB=![]() ,CM平分∠ACB
,CM平分∠ACB
∴∠ACM=∠BCM=![]() ,
,
∵∠ECD=![]() ,
,
∴∠ECF=∠DCF=![]() ,
,
∵CD=CE, CB=CB
∴△CBD≌△CBF(SAS)
∴BD=BE
∴CD=CE,
∵BC垂直平分线段DE,
∴BC⊥DE
(3) 当点D在线段BM上时,即△AFE≌△AMD时,AF=AM,
∵∠AFD=∠AMD=90°AD=AD,
∴Rt△ADF≌Rt△ADM(HL)
∴∠DAF=∠DAM=30°
∴∠DBA=∠DAB=30°
∴DA=DB
∵DF⊥AB
∴∠BDF=60°,BF=AF=2
BD=BE
∴△BDE是等边三角形,
∴DF=EF= BF·tan30°=![]()
DE=2EF=![]()
如图③-1中,当点D在BM的延长线时,易证AF=AM=2,DE=2DF=![]()
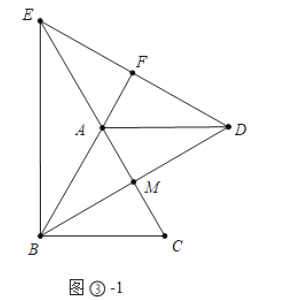
如图③-2中,当EF=AM=DF时,也满足条件,此时DE=BD=AB=4,
综上所述,满足条件的DE的值为![]() 或
或![]() 或4.
或4.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,等腰△ABC中,AB=AC,∠A=36°,△ABC绕点B逆时针方向旋转一定角度后到△BDE的位置,点D落在边AC上
问:(1)旋转角是几度?为什么?
(2)将AB与DE的交点记为F,除△ABC和△BDE外,图中还有几个等腰三角形?写出图中所有的等腰三角形
(3)请选择题(2)中找到的一个等腰三角形说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
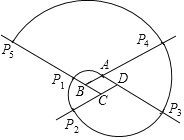
【题目】如图,四边形ABCD是边长为1的菱形,∠ABC=60°.动点P第1次从点A处开始,沿以B为圆心,AB为半径的圆弧运动到CB延长线,记为点P1;第2次从点P1开始,沿以C为圆心,CP1为半径的圆弧运动到DC的延长线,记为点P2;第3次从P2开始,沿以D为圆心,DP2为半径的圆弧运动到AD的延长线,记为点P3;第4次从点P3开始,沿以A为圆心,AP3为半径的圆弧运动到BA的延长线,记为点P4;…..如此运动下去,当点P运动到P20时,点P所运动的路程为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AD=BC,∠A=∠B,E为AB的中点,连结CE,DE.
(1)求证:△ADE≌△BCE.
(2)若∠A=70°,∠BCE=60°,求∠CDE的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
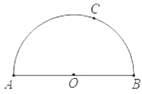
【题目】如图,![]() 为半圆
为半圆![]() 的直径,点
的直径,点![]() 为半圆上任一点.
为半圆上任一点.
(1)若![]() ,过点
,过点![]() 作半圆
作半圆![]() 的切线交直线
的切线交直线![]() 于点
于点![]() .求证:
.求证:![]() ;
;
(2)若![]() ,过点
,过点![]() 作
作![]() 的平行线交半圆
的平行线交半圆![]() 于点
于点![]() .当以点
.当以点![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形为菱形时,求
为顶点的四边形为菱形时,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
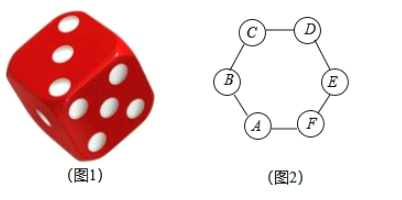
【题目】如图1,骰子有六个面并分别标有数1,2,3,4,5,6,如图2,正六边形![]() 顶点处各有一个圈,跳圈游戏的规则为:游戏者掷一次骰子,骰子向上的一面上的数字是几,就沿正六边形的边顺时针方向连续跳几个边长.
顶点处各有一个圈,跳圈游戏的规则为:游戏者掷一次骰子,骰子向上的一面上的数字是几,就沿正六边形的边顺时针方向连续跳几个边长.
如:若从圈![]() 起跳,第一次掷得3,就顺时针连续跳3个边长,落到圈
起跳,第一次掷得3,就顺时针连续跳3个边长,落到圈![]() ;若第二次掷得2,就从
;若第二次掷得2,就从![]() 开始顺时针连续跳2个边长,落到圈
开始顺时针连续跳2个边长,落到圈![]() ;……设游戏者从圈
;……设游戏者从圈![]() 起跳.
起跳.
(1)小明随机掷一次骰子,求落回到圈![]() 的概率
的概率![]() ;
;
(2)小亮随机掷两次骰子,用列表法或画树状图法求最后落回到圈![]() 的概率
的概率![]() ,并指出他与小明落回到圈
,并指出他与小明落回到圈![]() 的可能性一样吗?
的可能性一样吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为积极响应市委政府“加快建设天蓝水碧地绿的美丽长沙”的号召,我市某街道决定从备选的五种树中选购一种进行栽种.为了更好地了解社情民意,工作人员在街道辖区范围内随机抽取了部分居民,进行“我最喜欢的一种树”的调查活动(每人限选其中一种树),并将调查结果整理后,绘制成如图两个不完整的统计图:

请根据所给信息解答以下问题:
(1)这次参与调查的居民人数为: ;
(2)请将条形统计图补充完整;
(3)请计算扇形统计图中“枫树”所在扇形的圆心角度数;
(4)已知该街道辖区内现有居民8万人,请你估计这8万人中最喜欢玉兰树的有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校380名学生参加了这学期的“读书伴我行”活动,要求每人在这学期读书4~7本,活动结束后随机抽查了20名学生每人的读书量,并分为四种等级,![]() :4本;
:4本;![]() :5本;
:5本;![]() :6本;
:6本;![]() :7本.将各等级的人数绘制成尚不完整的扇形图和条形图.
:7本.将各等级的人数绘制成尚不完整的扇形图和条形图.
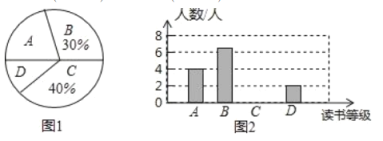
回答下列问题:
(1)补全条形图;这20名学生每人这学期读书量的众数是__________本,中位数是__________本;
(2)在求这20名学生这学期每人读书量的平均数时,小亮是这样计算的:
![]() (本).
(本).
小亮的计算是否正确?如果正确,估计这380名学生在这学期共读书多少本;如果不正确,请你帮他计算出正确的平均数,并估计这380名学生在这学期共读书多少本;
(3)若A等级的四名学生中有男生、女生各两名,现从中随机选出两名学生写读书感想,请用画树状图的方法求出刚好选中一名男生、一名女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现有5张除正面数字外完全相同的卡片,正面数字分别为1,2,3,4,5,将卡片背面朝上洗匀,从中随机抽出一张记下数字后放回,洗匀后再次随机抽出一张,则抽出的两张卡片上所写数字相同的概率______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com