
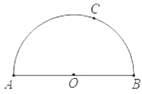
【题目】如图,![]() 为半圆
为半圆![]() 的直径,点
的直径,点![]() 为半圆上任一点.
为半圆上任一点.
(1)若![]() ,过点
,过点![]() 作半圆
作半圆![]() 的切线交直线
的切线交直线![]() 于点
于点![]() .求证:
.求证:![]() ;
;
(2)若![]() ,过点
,过点![]() 作
作![]() 的平行线交半圆
的平行线交半圆![]() 于点
于点![]() .当以点
.当以点![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形为菱形时,求
为顶点的四边形为菱形时,求![]() 的长.
的长.
【答案】(1)证明见解析;(2)![]() 或
或![]() .
.
【解析】
(1)由圆周角定理得到∠ACB=90°,先证△OAC是等边三角形,根据等边三角形和外角的性质得到∠OAP=∠BOC=120°,根据切线的性质得到∠OCP=90°,进一步得到∠ACP=∠OCB,最后根据全等三角形的判定定理证明即可;
(2)根据菱形的性质得到OA=AD=CD=OC,连接OD,得到△AOD与△COD是等边三角形,根据等边三角形的性质得到∠AOD=∠COD=60°,求得∠BOC=60°,根据弧长公式即可得到结论
解: (1)如图2∵AB为直径,
∴∠ACB=90°,
∴∠BAC=60°,
∴∠ABC=30°
∴AC=![]() AB=OA=OB=OC
AB=OA=OB=OC
∴△OAC是等边三角形
∴OC=AC,∠OAC=∠AOC=60°
∴∠CAP=∠BOC=120°
∴CP是⊙O的切线,
∴ OC⊥PC,
∴∠OCP=90°
∴∠ACP=∠OCB,
在△PBC与△AOC中,
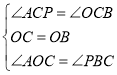
∴![]() (ASA)
(ASA)
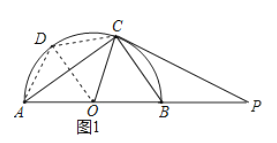
(2)如图1,连接OD,BD,CD
∵四边形AOCD是菱形
∴OA=AD=CD=OC,OA=OD=OC
∴△AOD与△COD是等边三角形,
∵.∠AOD=∠COD=60°,
∴∠BOC=60°,
∴![]()
同理:如图2可得: ![]()
故![]() 的长度为
的长度为![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
【题目】老师随机抽查了本学期学生读课外书册数的情况,绘制成条形图(图1)和不完整的扇形图(图2),其中条形图被墨迹遮盖了一部分.
(1)求条形图中被遮盖的数,并写出册数的中位数;
(2)在所抽查的学生中随机选一人谈读书感想,求选中读书超过5册的学生的概率;
(3)随后又补查了另外几人,得知最少的读了6册,将其与之前的数据合并后,发现册数的中位数没改变,则最多补查了 人.

查看答案和解析>>
科目:初中数学 来源: 题型:
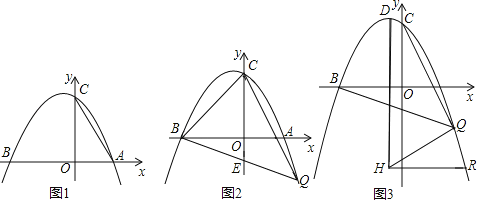
【题目】如图,抛物线y=ax2+bx+5经过坐标轴上A、B和C三点,连接AC,tanC=![]() ,5OA=3OB.
,5OA=3OB.
(1)求抛物线的解析式;
(2)点Q在第四象限的抛物线上且横坐标为t,连接BQ交y轴于点E,连接CQ、CB,△BCQ的面积为S,求S与t的函数解析式;
(3)已知点D是抛物线的顶点,连接CQ,DH所在直线是抛物线的对称轴,连接QH,若∠BQC=45°,HR∥x轴交抛物线于点R,HQ=HR,求点R的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,直线![]() 与x轴交于点B,与y轴交于点C,二次函数
与x轴交于点B,与y轴交于点C,二次函数![]() 的图象经过点B,C两点,且与x轴的负半轴交于点A,动点D在直线BC下方的二次函数图象上.
的图象经过点B,C两点,且与x轴的负半轴交于点A,动点D在直线BC下方的二次函数图象上.
(1)求二次函数的表达式;
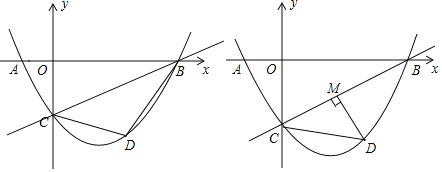
(2)如图1,连接DC,DB,设△BCD的面积为S,求S的最大值;
(3)如图2,过点D作DM⊥BC于点M,是否存在点D,使得△CDM中的某个角恰好等于∠ABC的2倍?若存在,直接写出点D的横坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某养殖场为了响应党中央的扶贫政策,今年起采用“场内+农户”养殖模式,同时加强对蛋鸡的科学管理,蛋鸡的产蛋率不断提高,三月份和五月份的产蛋量分别是2.5万kg与3.6万kg,现假定该养殖场蛋鸡产蛋量的月增长率相同.
(1)求该养殖场蛋鸡产蛋量的月平均增长率;
(2)假定当月产的鸡蛋当月在各销售点全部销售出去,且每个销售点每月平均销售量最多为0.32万kg.如果要完成六月份的鸡蛋销售任务,那么该养殖场在五月份已有的销售点的基础上至少再增加多少个销售点?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探究
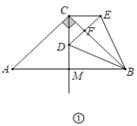
(1)如图①,在等腰直角三角形![]() 中,
中,![]() ,作
,作![]() 交
交![]() 于点
于点![]() ,点
,点![]() 为射线
为射线![]() 上一点,以点
上一点,以点![]() 为旋转中心将线段
为旋转中心将线段![]() 逆时针旋转90°得到线段
逆时针旋转90°得到线段![]() ,连接
,连接![]() 交射线
交射线![]() 于点
于点![]() ,连接
,连接![]() 、
、![]() .
.
填空:
①线段![]() 、
、![]() 的数量关系为___________.
的数量关系为___________.
②线段![]() 、
、![]() 的位置关系为___________.
的位置关系为___________.
推广:
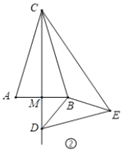
(2)如图②,在等腰三角形![]() 中,
中,![]() ,作
,作![]() 交
交![]() 于点
于点![]() ,点
,点![]() 为
为![]() 外部射线
外部射线![]() 上一点,以点
上一点,以点![]() 为旋转中心将线段
为旋转中心将线段![]() 逆时针旋转
逆时针旋转![]() 度得到线段
度得到线段![]() ,连接
,连接![]() 、
、![]() 、
、![]() 请判断(1)中的结论是否成立,并说明理由.
请判断(1)中的结论是否成立,并说明理由.
应用:
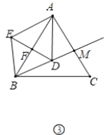
(3)如图③,在等边三角形![]() 中,
中,![]() .作
.作![]() 交
交![]() 于点
于点![]() ,点
,点![]() 为射线
为射线![]() 上一点,以点
上一点,以点![]() 为旋转中心将线段
为旋转中心将线段![]() 逆时针旋转60°得到线段
逆时针旋转60°得到线段![]() ,连接
,连接![]() 交射线
交射线![]() 于点
于点![]() ,连接
,连接![]() 、
、![]() .当以
.当以![]() 、
、![]() 、
、![]() 为顶点的三角形与
为顶点的三角形与![]() 全等时,请直接写出
全等时,请直接写出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
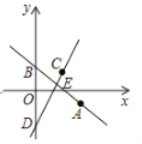
【题目】如图,在平面直角坐标系中,直线![]() 过点
过点![]() 且与
且与![]() 轴交于点
轴交于点![]() .把点
.把点![]() 向左平移2个单位,再向上平移4个单位,得到点
向左平移2个单位,再向上平移4个单位,得到点![]() .过点
.过点![]() 的直线
的直线![]() 交
交![]() 轴于点
轴于点![]() .
.
(1)求直线![]() 的解析式.
的解析式.
(2)直线![]() 与
与![]() 交于点
交于点![]() ,在直线
,在直线![]() 和直线
和直线![]() 上是否存在点
上是否存在点![]() ,使
,使![]() ,若存在,求出点
,若存在,求出点![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
(3)若有过点![]() 的直线
的直线![]() 与线段
与线段![]() 有公共点且满足
有公共点且满足![]() 随
随![]() 的增大而减小,设直线
的增大而减小,设直线![]() 与
与![]() 轴交点横坐标为
轴交点横坐标为![]() ,直接写出
,直接写出![]() 的取值范围________.
的取值范围________.
查看答案和解析>>
科目:初中数学 来源: 题型:
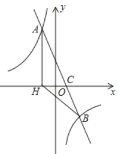
【题目】如图,在平面直角坐标系中,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于
的图象交于![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,过点
,过点![]() 作
作![]() 轴于点
轴于点![]() ,点
,点![]() 是线段
是线段![]() 的中点,
的中点,![]() ,
,![]() ,点
,点![]() 的坐标为
的坐标为![]() .
.
(1)求该反比例函数和一次函数的解析式;
(2)求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地区一种商品的需求量y1(单位:万件)、供应量y2(单位;万件)与价格x(单位:元/件)分别近似满足下列函数关系式:y1=-x+60,y2=2x-36.需求量为0时,即停止供应.当y1=y2时,该商品的价格称为稳定价格,需求量称为稳定需求量.
(1)求该商品的稳定价格与稳定需求量;
(2)价格在什么范围时,该商品的需求量低于供应量;
(3)当需求量高于供应量时,政府常通过对供应方提供价格补贴来提高供货价格,以提高供应量.现若要使稳定需求量增加4万件,政府应对每件商品提供多少元补贴才能使供应量等于需求量?
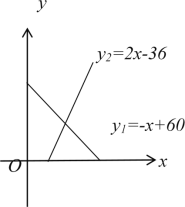
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com