
【题目】如图,在平面直角坐标系中,直线![]() 过点
过点![]() 且与
且与![]() 轴交于点
轴交于点![]() .把点
.把点![]() 向左平移2个单位,再向上平移4个单位,得到点
向左平移2个单位,再向上平移4个单位,得到点![]() .过点
.过点![]() 的直线
的直线![]() 交
交![]() 轴于点
轴于点![]() .
.
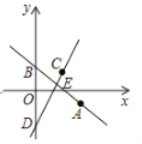
(1)求直线![]() 的解析式.
的解析式.
(2)直线![]() 与
与![]() 交于点
交于点![]() ,在直线
,在直线![]() 和直线
和直线![]() 上是否存在点
上是否存在点![]() ,使
,使![]() ,若存在,求出点
,若存在,求出点![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
(3)若有过点![]() 的直线
的直线![]() 与线段
与线段![]() 有公共点且满足
有公共点且满足![]() 随
随![]() 的增大而减小,设直线
的增大而减小,设直线![]() 与
与![]() 轴交点横坐标为
轴交点横坐标为![]() ,直接写出
,直接写出![]() 的取值范围________.
的取值范围________.
【答案】(1)![]() ;(2)存在,
;(2)存在,![]() 或
或![]() ;(3)
;(3)![]() ,
,![]()
【解析】
(1)将![]() 代入直线
代入直线![]() 求出其坐标后,根据点平移与坐标的变化求出点
求出其坐标后,根据点平移与坐标的变化求出点![]() ,代入直线
,代入直线![]() 即可得解.
即可得解.
(2)联立两直线解析式求出![]() 点坐标,进而求得
点坐标,进而求得![]() 的面积,令
的面积,令![]() ,即可解得
,即可解得![]() 到
到![]() 轴的距离,代入两直线解析式即可求得两个答案.
轴的距离,代入两直线解析式即可求得两个答案.
(3)有两种情况,第一种,由于直线![]() 满足
满足![]() 随
随![]() 的增大而减小,根据一次函数的性质,可得
的增大而减小,根据一次函数的性质,可得![]() ,且直线过点
,且直线过点![]() ,故
,故![]() ;该直线与线段
;该直线与线段![]() 有公共点,其最大值即直线
有公共点,其最大值即直线![]() 与
与![]() 轴的交点,解之即可.第二种最小值为直线
轴的交点,解之即可.第二种最小值为直线![]() 与
与![]() 轴的交点,无上限,求得
轴的交点,无上限,求得![]() 的解析式后令
的解析式后令![]() ,解之即可.
,解之即可.
(1)把![]() 代入
代入![]() 得
得![]() ,则
,则![]() ,
,
∵点![]() 向左平移2个单位,再向上平移4个单位,得到点
向左平移2个单位,再向上平移4个单位,得到点![]() ,
,
∴![]() .
.
将点![]() 代入
代入![]() , 得
, 得![]() ,解得
,解得![]() ,
,
∴直线![]() 的解析式为
的解析式为![]() ;
;
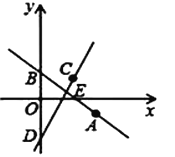
(2)令![]() ,
,
解得![]()
∵![]()
∴![]()
把![]() 代入
代入![]()
把![]() 代入
代入![]()
综上,![]() 或
或![]()
(3)第一种情况:
因为直线![]() 满足
满足![]() 随
随![]() 的增大而减小,故
的增大而减小,故![]() ,
,
直线![]() 过点
过点![]() ,故直线
,故直线![]() 与
与![]() 轴交点横坐标
轴交点横坐标![]() ,
,
当直线![]() 过
过![]() ,
,![]() 时,与
时,与![]() 轴交点横坐标取最大值,
轴交点横坐标取最大值,
此时![]() ,
,
解得![]()
所以直线解析式为![]() ,
,
令![]() ,解得
,解得![]() ,
,
故直线![]() 与
与![]() 轴交点横坐标取值范围为
轴交点横坐标取值范围为![]() .
.
第二种情况:
当直线![]() 过
过![]() ,
,![]() 时,与
时,与![]() 轴交点横坐标取最小值,
轴交点横坐标取最小值,
此时![]()
解得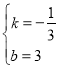
所以直线解析式为![]() ,
,
令![]() ,解得
,解得![]() ,
,
故直线![]() 与
与![]() 轴交点横坐标取值范围为
轴交点横坐标取值范围为![]() .
.
综上,直线![]() 与
与![]() 轴交点横坐标取值范围为
轴交点横坐标取值范围为![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
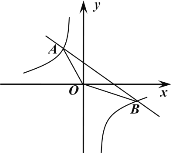
【题目】已知一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象相交于A、B两点,坐标分别为
的图象相交于A、B两点,坐标分别为![]() 、
、![]() .
.
(1)求两个函数的解析式;
(2)结合图象写出![]() 时,x的取值范围;
时,x的取值范围;
(3)求△AOB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在矩形ABCD中,AB=8,点H是直线AB边上的一个点,连接DH交直线CB的干点E,交直线AC于点F,连接BF.
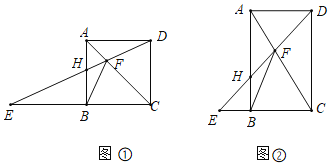
(1)如图①,点H在AB边上,若四边形ABCD是正方形,求证:△ADF≌△ABF;
(2)在(1)的条件下,若△BHF为等腰三角形,求HF的长;
(3)如图②,若tan∠ADH=![]() ,是否存在点H,使得△BHF为等腰三角形?若存在,求该三角形的腰长;若不存在,试说明理由.
,是否存在点H,使得△BHF为等腰三角形?若存在,求该三角形的腰长;若不存在,试说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 为半圆
为半圆![]() 的直径,点
的直径,点![]() 为半圆上任一点.
为半圆上任一点.
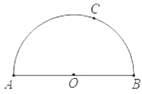
(1)若![]() ,过点
,过点![]() 作半圆
作半圆![]() 的切线交直线
的切线交直线![]() 于点
于点![]() .求证:
.求证:![]() ;
;
(2)若![]() ,过点
,过点![]() 作
作![]() 的平行线交半圆
的平行线交半圆![]() 于点
于点![]() .当以点
.当以点![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形为菱形时,求
为顶点的四边形为菱形时,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】连接正八边形的三个顶点,得到如图所示的图形,下列说法错误的是( )

A. ![]() 是等边三角形
是等边三角形
B. 连接![]() ,则
,则![]() 分别平分
分别平分![]() 和
和![]()
C. 整个图形是轴对称图形,但不是中心对称图形
D. 四边形![]() 与四边形
与四边形![]() 的面积相等
的面积相等
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为积极响应市委政府“加快建设天蓝水碧地绿的美丽长沙”的号召,我市某街道决定从备选的五种树中选购一种进行栽种.为了更好地了解社情民意,工作人员在街道辖区范围内随机抽取了部分居民,进行“我最喜欢的一种树”的调查活动(每人限选其中一种树),并将调查结果整理后,绘制成如图两个不完整的统计图:

请根据所给信息解答以下问题:
(1)这次参与调查的居民人数为: ;
(2)请将条形统计图补充完整;
(3)请计算扇形统计图中“枫树”所在扇形的圆心角度数;
(4)已知该街道辖区内现有居民8万人,请你估计这8万人中最喜欢玉兰树的有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,AC=6![]() ,BD=6,E是BC边的中点,P,M分别是AC,AB上的动点,连接PE,PM,则PE+PM的最小值是( )
,BD=6,E是BC边的中点,P,M分别是AC,AB上的动点,连接PE,PM,则PE+PM的最小值是( )

A. 6 B. 3![]() C. 2
C. 2![]() D. 4.5
D. 4.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以AD为直径的半圆O经过Rt△ABC斜边AB的两个端点,交直角边AC于点E,B、E是半圆弧的三等分点,弧BE的长为![]() π,则图中阴影部分的面积为( )
π,则图中阴影部分的面积为( )
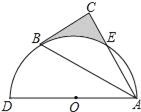
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
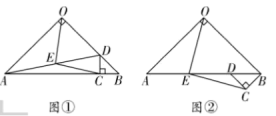
【题目】如图①,在![]() 中,
中,![]() 为
为![]() 边上一点,过
边上一点,过![]() 点作
点作![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,
,![]() 为
为![]() 的中点,连接
的中点,连接![]() .
.
(观察猜想)
(1)①![]() 的数量关系是___________
的数量关系是___________
②![]() 的数量关系是______________
的数量关系是______________
(类比探究)
(2)将图①中![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() ,如图②所示,则(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由;
,如图②所示,则(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由;
(拓展迁移)
(3)将![]() 绕点
绕点![]() 旋转任意角度,若
旋转任意角度,若![]() ,请直接写出点
,请直接写出点![]() 在同一直线上时
在同一直线上时![]() 的长.
的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com