
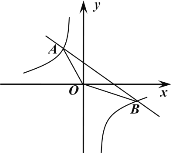
【题目】已知一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象相交于A、B两点,坐标分别为
的图象相交于A、B两点,坐标分别为![]() 、
、![]() .
.
(1)求两个函数的解析式;
(2)结合图象写出![]() 时,x的取值范围;
时,x的取值范围;
(3)求△AOB的面积.
【答案】(1)![]() ;
;![]() ;(2)-2<x<0或x>4;(3)6.
;(2)-2<x<0或x>4;(3)6.
【解析】
(1)直接利用待定系数法可分别求得两个函数的解析式;
(2)利用交点坐标,结合图形可写出x的取值范围;
(3)把△AOB的面积分为两部分,即S△AOB=S△AOC+S△BOC.
解:(1)把点A(-2,4)代入解析式![]() 中,得k=-8,
中,得k=-8,
即双曲线解析式为y=![]()
分别把点A(-2,4),B(4,-2)代入解析式![]() ,得
,得
![]()
解得![]()
∴直线解析式为y=-x+2.
∴![]() ;
;![]()
(2)∵一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象相交于A、B两点,坐标分别为
的图象相交于A、B两点,坐标分别为![]() 、
、![]()
∴当![]() 时,-2<x<0或x>4.
时,-2<x<0或x>4.
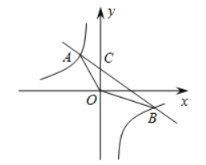
(3)当x=0时,y=-x+2=2,即OC=2
∴S△AOB=S△AOC+S△BOC=![]() ×2×2+
×2×2+![]() ×2×4=6.
×2×4=6.
故答案为(1)![]() ;
;![]() ;(2)-2<x<0或x>4;(3)6.
;(2)-2<x<0或x>4;(3)6.


 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案科目:初中数学 来源: 题型:
【题目】“低碳生活,绿色出行”是我们倡导的一种生活方式,有关部门抽样调查了某单位员工上下班的交通方式,绘制了两幅统计图:
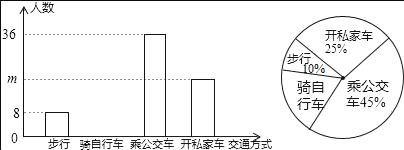
(1)样本中的总人数为 人;扇形统计十图中“骑自行车”所在扇形的圆心角为 度;
(2)补全条形统计图;
(3)该单位共有1000人,积极践行这种生活方式,越来越多的人上下班由开私家车改为骑自行车.若步行,坐公交车上下班的人数保持不变,问原来开私家车的人中至少有多少人改为骑自行车,才能使骑自行车的人数不低于开私家车的人数?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近两年购物的支付方式日益增多,某数学兴趣小组就此进行了抽样调查,调查结果显示,支付方式有:A微信.B支付宝.C银行卡.D其他.该小组选取了某一超市一天之内购买者的支付方式进行统计,得到如下两幅不完整的统计图.
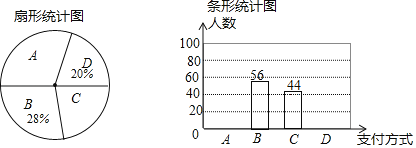
请你根据统计图提供的信息,解答下列问题:
(1)本次调查中,一共调查了多少名购买者?
(2)补全条形统计图:“A微信”支付方式所在扇形的圆心角为 度;
(3)若该超市这一天内有2000名购买者,请你估计B种支付方式的购买者有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】老师随机抽查了本学期学生读课外书册数的情况,绘制成条形图(图1)和不完整的扇形图(图2),其中条形图被墨迹遮盖了一部分.
(1)求条形图中被遮盖的数,并写出册数的中位数;
(2)在所抽查的学生中随机选一人谈读书感想,求选中读书超过5册的学生的概率;
(3)随后又补查了另外几人,得知最少的读了6册,将其与之前的数据合并后,发现册数的中位数没改变,则最多补查了 人.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解初三学生的体育锻炼时间,小华调查了某班45名同学一周参加体育锻炼的情况,并把它绘制成折线统计图(如图所示).那么关于该班45名同学一周参加体育锻炼时间的说法错误的是( )
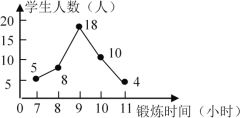
A.众数是9
B.中位数是9
C.平均数是9
D.锻炼时间不低于9小时的有14人
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某汽车租赁公司对某款汽车的租赁方式按时段计费,该公司要求租赁方必须在9天内(包括9天)将所租汽车归还.租赁费用![]() (元)随时间
(元)随时间![]() (天)的变化图象为折线
(天)的变化图象为折线![]() ,如图所示.
,如图所示.
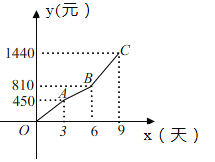
(1)当租赁时间不超过3天时,求每日租金.
(2)当![]() 时,求
时,求![]() (元)与
(元)与![]() (天)的函数关系式.
(天)的函数关系式.
(3)甲、乙两人租赁该款汽车各一辆,两人租赁的时间共为9天,甲租的天数少于3天,乙比甲多支付费用720元.请问乙租这款汽车多长时间?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知等边△ABC的边长是2,以BC边上的高AB1为边作等边三角形,得到第一个等边△AB1C1;再以等边△AB1C1的B1C1边上的高AB2为边作等边三角形,得到第二个等边△AB2C2;再以等边△AB2C2的B2C2边上的高AB3为边作等边三角形,得到第三个等边△AB3C3;…,记△B1CB2的面积为S1,△B2C1B3的面积为S2,△B3C2B4的面积为S3,如此下去,则Sn=_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+5经过坐标轴上A、B和C三点,连接AC,tanC=![]() ,5OA=3OB.
,5OA=3OB.
(1)求抛物线的解析式;
(2)点Q在第四象限的抛物线上且横坐标为t,连接BQ交y轴于点E,连接CQ、CB,△BCQ的面积为S,求S与t的函数解析式;
(3)已知点D是抛物线的顶点,连接CQ,DH所在直线是抛物线的对称轴,连接QH,若∠BQC=45°,HR∥x轴交抛物线于点R,HQ=HR,求点R的坐标.
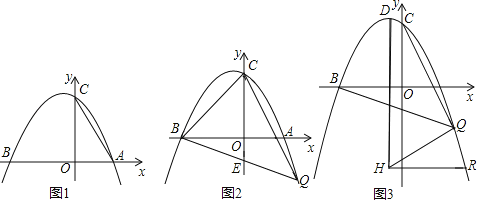
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线![]() 过点
过点![]() 且与
且与![]() 轴交于点
轴交于点![]() .把点
.把点![]() 向左平移2个单位,再向上平移4个单位,得到点
向左平移2个单位,再向上平移4个单位,得到点![]() .过点
.过点![]() 的直线
的直线![]() 交
交![]() 轴于点
轴于点![]() .
.
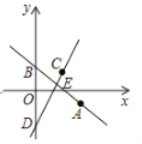
(1)求直线![]() 的解析式.
的解析式.
(2)直线![]() 与
与![]() 交于点
交于点![]() ,在直线
,在直线![]() 和直线
和直线![]() 上是否存在点
上是否存在点![]() ,使
,使![]() ,若存在,求出点
,若存在,求出点![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
(3)若有过点![]() 的直线
的直线![]() 与线段
与线段![]() 有公共点且满足
有公共点且满足![]() 随
随![]() 的增大而减小,设直线
的增大而减小,设直线![]() 与
与![]() 轴交点横坐标为
轴交点横坐标为![]() ,直接写出
,直接写出![]() 的取值范围________.
的取值范围________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com