
【题目】近两年购物的支付方式日益增多,某数学兴趣小组就此进行了抽样调查,调查结果显示,支付方式有:A微信.B支付宝.C银行卡.D其他.该小组选取了某一超市一天之内购买者的支付方式进行统计,得到如下两幅不完整的统计图.
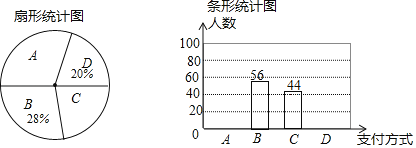
请你根据统计图提供的信息,解答下列问题:
(1)本次调查中,一共调查了多少名购买者?
(2)补全条形统计图:“A微信”支付方式所在扇形的圆心角为 度;
(3)若该超市这一天内有2000名购买者,请你估计B种支付方式的购买者有多少人?
【答案】(1)200(人); (2)图见解析;108;(3)560人.
【解析】
(1)根据B的数量和所占的百分比可以求得本次调查的购买者的人数;
(2)根据统计图中的数据可以求得选择A和D的人数,从而可以将条形统计图补充完整,求得在扇形统计图中A种支付方式所对应的圆心角的度数;
(3)根据统计图中的数据可以计算出使用A和B两种支付方式的购买者共有多少名.
解:(1)一共调查的购买者人数为:56÷28%=200(人)
答:本次调查中,一共调查了200名购买者;
(2)D类人数为:200×20%=40(人),
则A类人数为:200﹣56﹣44﹣40=60
补全条形统计图如图所示:
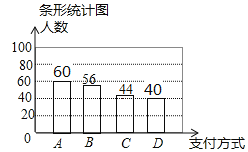
“A微信”支付方式所在扇形的圆心角为:360°×![]() ×100%=108°,
×100%=108°,
故答案为:108;
(3)B种支付方式的购买者:2000×28%=560,
答:B种支付方式的购买者有560人.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某商场计划用3 800元购进节能灯120只,这两种节能灯的进价、售价如下表:
进价(元/只) | 售价(元/只) | |
甲型 | 25 | 30 |
乙型 | 45 | 60 |
(1)求甲、乙两种节能灯各进多少只?
(2)全部售完120只节能灯后,该商场获利润多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
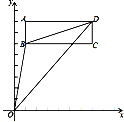
【题目】如图,在长方形ABCD中,点A(1,8),B(1,6),C(7,6).
(1)请直接写出点D的坐标;
(2)连接线段OB,OD,BD,请求出△OBD的面积;
(3)若长方形ABCD以每秒1个单位长度的速度向下运动,设运动的时间为t秒,是否存在某一时刻,使△OBD的面积与长方形ABCD的面积相等?若存在,请求出t的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB∥CD,EG、EM、FM分别平分∠AEF,∠BEF,∠EFD,则下列结论正确的有( )
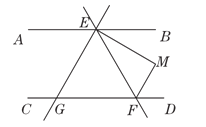
①∠DFE=∠AEF;②∠EMF=90°;③EG∥FM;④∠AEF=∠EGC.
A. 1个B. 2个
C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
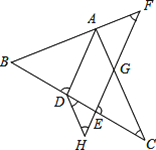
【题目】如图,AD平分∠BAC交BC于点D,点F在BA的延长线上,点E在线段CD上,EF与AC相交于点G,∠BDA+∠CEG=180°.
(1)AD与EF平行吗?请说明理由;
(2)若点H在FE的延长线上,且∠EDH=∠C,则∠F与∠H相等吗,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明用12元买软面笔记本,小丽用21元买硬面笔记本.
(1)已知每本硬面笔记本比软面笔记本贵1.2元,小明和小丽能买到相同数量的笔记本吗?
(2)已知每本硬面笔记本比软面笔记本贵a元,是否存在正整数a,使得每本硬面笔记本、软面笔记本的价格都是正整数,并且小明和小丽能买到相同数量的笔记本?若存在,求出a的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲乙两家绿化养护公司各自推出了校园绿化养护服务的收费方案.
甲公司方案:每月的养护费用y(元)与绿化面积x(平方米)是一次函数关系,如图所示.
乙公司方案:绿化面积不超过1000平方米时,每月收取费用5500元;绿化面积超过1000平方米时,每月在收取5500元的基础上,超过部分每平方米收取4元.

(1)求如图所示的y与x的函数解析式;(不要求写取值范围)
(2)如果某学校目前的绿化面积是1200平方米.试通过计算说明:选择哪家公司的服务,每月的绿化养护费用较少.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c的图象交x轴于A(﹣1,0),B(2,0),交y轴于C(0,﹣2),过A,C画直线.
(1)求二次函数的解析式;
(2)点P在x轴正半轴上,且PA=PC,求OP的长;
(3)点M在二次函数图象上,以M为圆心的圆与直线AC相切,切点为H.
①若M在y轴右侧,且△CHM∽△AOC(点C与点A对应),求点M的坐标;
②若⊙M的半径为![]() ,求点M的坐标.
,求点M的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新知:对角线垂直的四边形两组对边的平方和相等
感知与认证:如图1,2,3中,四边形ABCD中![]() 于O,如图1,AC与BD相互平分,如图2,AC平分BD,结论显然成立.
于O,如图1,AC与BD相互平分,如图2,AC平分BD,结论显然成立.
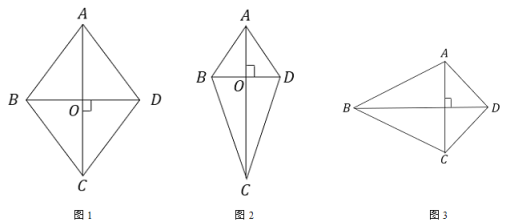
认知证明:(1)请你证明如图3中有![]() 成立。
成立。
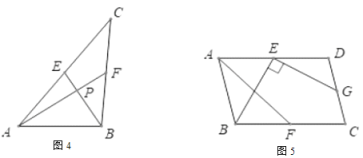
发现应用:(2)如图4,若AF,BE是三角形ABC的中线,![]() 垂足为P
垂足为P
已知:![]() ,
,![]() ,求AB的长
,求AB的长
拓展应用:(3)如图5,在平行四边形ABCD中,点E,F,G分别是AD,BC,CD的中点,![]() ,
,![]() ,
,![]() .求AF的长.
.求AF的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com