
【题目】如图,AB∥CD,EG、EM、FM分别平分∠AEF,∠BEF,∠EFD,则下列结论正确的有( )
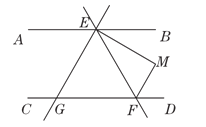
①∠DFE=∠AEF;②∠EMF=90°;③EG∥FM;④∠AEF=∠EGC.
A. 1个B. 2个
C. 3个D. 4个
【答案】C
【解析】
根据角平分线的定义,平行线的性质和判定解答即可.
∵AB∥CD,∴∠DFE=∠AEF(两直线平行,内错角相等),①正确;
∵AB∥CD, ∴∠MFE+∠MEF=180°,
∵FM平分∠EFD,EM平分∠BEF,
∴∠MFE=![]() ∠DFE,∠MEF =
∠DFE,∠MEF =![]() ∠BEF,
∠BEF,
∴∠EMF=∠MFE+∠MEF = ![]() ∠DFE+
∠DFE+![]() ∠BEF=90°, ②正确;
∠BEF=90°, ②正确;
∵AB∥CD, ∴∠AEF=∠DFE,
∵EG平分∠AEF,
∴∠AEG=∠GEF=![]() ∠AEF,
∠AEF,
∵FM平分∠DFE,
∴∠EFM=∠MFD=![]() ∠DFE,
∠DFE,
∴∠GEF=∠EFM, ∴EG∥FM,③正确;
∵∠AEF=∠DFE≠∠EGC,④错误,正确的有3个,
故选:C.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】已知整数a1,a2,a3,a4,┈满足下列条件;a1=0,a2=-|a1+1|,a3=-|a2+2|,a4=-|a3+3|,┈,依次类推,则a2012 的值为( )
A.-2012B.-1005C.-1006D.-1007
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,点![]() 是第一象限内的点,直线
是第一象限内的点,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,过点
,过点![]() 作
作![]() 轴,垂足为
轴,垂足为![]() ,过点
,过点![]() 的直线与
的直线与![]() 轴交于点
轴交于点![]() ,已知直线
,已知直线![]() 上的点的坐标
上的点的坐标![]() 是方程的
是方程的![]() 解,直线
解,直线![]() 上的点的坐标
上的点的坐标![]() 是方程
是方程![]() 的解
的解
(1)求点![]() 的坐标
的坐标
(2)证明:![]() (要求写出每一步的推理依据);
(要求写出每一步的推理依据);
(3)求点![]() 的坐标,并求三角形
的坐标,并求三角形![]() 的面积
的面积

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB是⊙O的弦,半径OA=2cm,∠AOB=120°

(1)求tan∠OAB的值;
(2)求图中阴影部分的面积S;
(3)在⊙O上一点P从A点出发,沿逆时针方向运动一周,回到点A,在点P的运动过程中,满足S△POA=S△AOB时,直接写出P点所经过的弧长(不考虑点P与点B重合的情形).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】背景情境:
赛赛同学在学习《一元二次方程》中做过这样一道题:
题目:已知实数![]() 、
、![]() 满足
满足![]() ,
,![]() ,且
,且![]() ,求
,求![]() 的值.
的值.
解:根据题意得
![]() 与
与![]() 为方程
为方程![]() 的两根,
的两根,
∴![]() ,
,![]()
∴![]()
请认真阅读赛赛同学解题的方法,仔细思考.
解决问题:
(1)已知实数![]() 、
、![]() 满足
满足![]() ,
,![]() ,且
,且![]() ,求
,求![]() 的值.
的值.
(2)设实数![]() 、
、![]() 分别满足
分别满足![]() ,
,![]() ,且
,且![]() ,求
,求![]() 的值.
的值.
(3)已知关于![]() 的方程
的方程![]() 有两个根
有两个根![]() 、
、![]() 满足
满足![]() .当
.当![]() 的三边
的三边![]() 、
、![]() 、
、![]() 满足
满足![]() ,
,![]() ,
,![]() (a≠b).求
(a≠b).求![]() 的值以及
的值以及![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=mx+4的图象与x轴相交于点A,与反比例函数y=![]() (x>0)的图象相交于点B(1,6).
(x>0)的图象相交于点B(1,6).
(1)求一次函数和反比例函数的解析式;
(2)设点P是x轴上一点,若S△APB=18,直接写出点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近两年购物的支付方式日益增多,某数学兴趣小组就此进行了抽样调查,调查结果显示,支付方式有:A微信.B支付宝.C银行卡.D其他.该小组选取了某一超市一天之内购买者的支付方式进行统计,得到如下两幅不完整的统计图.
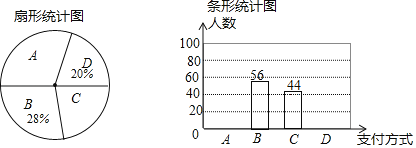
请你根据统计图提供的信息,解答下列问题:
(1)本次调查中,一共调查了多少名购买者?
(2)补全条形统计图:“A微信”支付方式所在扇形的圆心角为 度;
(3)若该超市这一天内有2000名购买者,请你估计B种支付方式的购买者有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,CA⊥AB,垂足为 A,AB=24,AC=12,射线 BM⊥AB,垂足为 B, 一动点 E 从 A点出发以 3 厘米/秒沿射线 AN 运动,点 D 为射线 BM 上一动点, 随着 E 点运动而运动,且始终保持 ED=CB,当点 E 经过______秒时,△DEB 与△BCA 全等.
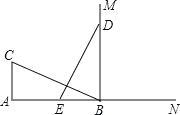
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com