
【题目】背景情境:
赛赛同学在学习《一元二次方程》中做过这样一道题:
题目:已知实数![]() 、
、![]() 满足
满足![]() ,
,![]() ,且
,且![]() ,求
,求![]() 的值.
的值.
解:根据题意得
![]() 与
与![]() 为方程
为方程![]() 的两根,
的两根,
∴![]() ,
,![]()
∴![]()
请认真阅读赛赛同学解题的方法,仔细思考.
解决问题:
(1)已知实数![]() 、
、![]() 满足
满足![]() ,
,![]() ,且
,且![]() ,求
,求![]() 的值.
的值.
(2)设实数![]() 、
、![]() 分别满足
分别满足![]() ,
,![]() ,且
,且![]() ,求
,求![]() 的值.
的值.
(3)已知关于![]() 的方程
的方程![]() 有两个根
有两个根![]() 、
、![]() 满足
满足![]() .当
.当![]() 的三边
的三边![]() 、
、![]() 、
、![]() 满足
满足![]() ,
,![]() ,
,![]() (a≠b).求
(a≠b).求![]() 的值以及
的值以及![]() 的面积.
的面积.
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】在⊙O中,直径AB=6,BC是弦,∠ABC=30°,点P在BC上,点Q在⊙O上,且OP⊥PQ.
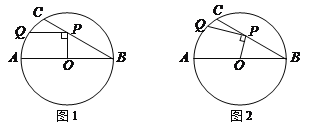
(1)如图1,当PQ∥AB时,求PQ的长度;
(2)如图2,当点P在BC上移动时,求PQ长的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
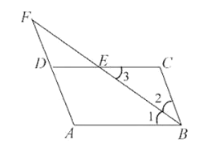
【题目】如图,在四边形![]() 中,
中,![]() 的平分线交
的平分线交![]() 于点
于点![]() ,交
,交![]() 的延长线于点
的延长线于点![]() ,
,![]()
(1)写出![]() 对由条件
对由条件![]() 推出的相等或互补的角
推出的相等或互补的角
(2)![]() 与
与![]() 相等吗?为什么?
相等吗?为什么?
(3)证明:![]()
请在下面的括号内,填上推理的根据,并完成下面的证明:
![]() ( ① )
( ① )
![]() (已证),
(已证),![]() ,( ② )
,( ② )
又![]() (角平分线的定义)
(角平分线的定义)
![]() ( ③ )
( ③ )
查看答案和解析>>
科目:初中数学 来源: 题型:
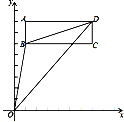
【题目】如图,在长方形ABCD中,点A(1,8),B(1,6),C(7,6).
(1)请直接写出点D的坐标;
(2)连接线段OB,OD,BD,请求出△OBD的面积;
(3)若长方形ABCD以每秒1个单位长度的速度向下运动,设运动的时间为t秒,是否存在某一时刻,使△OBD的面积与长方形ABCD的面积相等?若存在,请求出t的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB∥CD,EG、EM、FM分别平分∠AEF,∠BEF,∠EFD,则下列结论正确的有( )
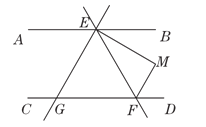
①∠DFE=∠AEF;②∠EMF=90°;③EG∥FM;④∠AEF=∠EGC.
A. 1个B. 2个
C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
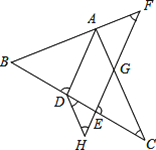
【题目】如图,AD平分∠BAC交BC于点D,点F在BA的延长线上,点E在线段CD上,EF与AC相交于点G,∠BDA+∠CEG=180°.
(1)AD与EF平行吗?请说明理由;
(2)若点H在FE的延长线上,且∠EDH=∠C,则∠F与∠H相等吗,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲乙两家绿化养护公司各自推出了校园绿化养护服务的收费方案.
甲公司方案:每月的养护费用y(元)与绿化面积x(平方米)是一次函数关系,如图所示.
乙公司方案:绿化面积不超过1000平方米时,每月收取费用5500元;绿化面积超过1000平方米时,每月在收取5500元的基础上,超过部分每平方米收取4元.

(1)求如图所示的y与x的函数解析式;(不要求写取值范围)
(2)如果某学校目前的绿化面积是1200平方米.试通过计算说明:选择哪家公司的服务,每月的绿化养护费用较少.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com