【题目】已知一次函数图像经过
和
两点
（1）求这个函数解析式；
（2）过点B作直线与
轴交于点
，若三角形
的面积为10，试求点P的坐标．
科目：初中数学 来源： 题型：
【题目】如图，AB∥CD，EG、EM、FM分别平分∠AEF，∠BEF，∠EFD，则下列结论正确的有( )
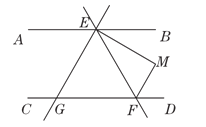
①∠DFE＝∠AEF；②∠EMF＝90°；③EG∥FM；④∠AEF＝∠EGC.
A. 1个B. 2个
C. 3个D. 4个
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，二次函数y=ax2+bx+c的图象交x轴于A（﹣1，0），B（2，0），交y轴于C（0，﹣2），过A，C画直线．
（1）求二次函数的解析式；
（2）点P在x轴正半轴上，且PA=PC，求OP的长；
（3）点M在二次函数图象上，以M为圆心的圆与直线AC相切，切点为H．
①若M在y轴右侧，且△CHM∽△AOC（点C与点A对应），求点M的坐标；
②若⊙M的半径为
，求点M的坐标．
查看答案和解析>>
科目：初中数学 来源： 题型：
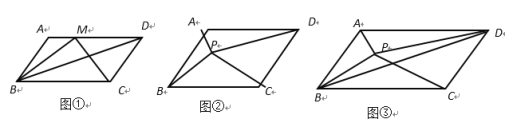
【题目】我们知道：平行四边形的面积＝(底边)×(这条底边上的高)．如图，四边形ABCD都是平行四边形，AD∥BC，AB∥CD，设它的面积为S．
（1）如图①，点M为AD上任意一点，若△BCM的面积为S1，则S1：S＝ ；
（2）如图②，点P为平行四边形ABCD内任意一点时，记△PAB的面积为Sˊ，△PCD的面积为S〞，平行四边形ABCD的面积为S，猜想得Sˊ、S〞的和与S的数量关系式为 ；
（3）如图③，已知点P为平行四边形ABCD内任意一点，△PAB的面积为3，△PBC的面积为7，求△PBD的面积．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】阅读下列材料：
“ a 2 ≥0”这个结论在数学中非常有用，有时我们需要将代数式配成完全平方式．例如：
x2 4x 5 x2 4x 4 1 x 22 1 ，
∵ x 22 ≥0，
∴ x 22 1 ≥1，
∴ x2 4x 5 ≥1.
试利用“配方法”解决下列问题：
(1)填空： x2 4x 5 ( x )2＋ ；
(2)已知 x2 4x y2 2y 5 0 ，求 x y 的值；
(3)比较代数式 x2 1与2x 3 的大小．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】新知：对角线垂直的四边形两组对边的平方和相等
感知与认证：如图1，2，3中，四边形ABCD中
于O，如图1，AC与BD相互平分，如图2，AC平分BD,结论显然成立.
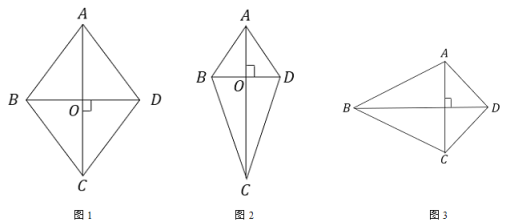
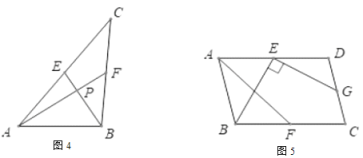
认知证明：（1）请你证明如图3中有
成立。
发现应用：（2）如图4，若AF,BE是三角形ABC的中线，
垂足为P
已知：
,
,求AB的长
拓展应用：（3）如图5，在平行四边形ABCD中，点E,F,G分别是AD,BC,CD的中点，
,
，
.求AF的长.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图1，AB为半圆O的直径，D为BA的延长线上一点，DC为半圆O的切线，切点为C．
（1）求证：∠ACD=∠B；
（2）如图2，∠BDC的平分线分别交AC，BC于点E，F；
①求tan∠CFE的值；
②若AC=3，BC=4，求CE的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某工厂甲、乙两个部门各有员工400人，为了解这两个部门员工的生产技能情况，进行了抽样调查，过程如下，请补充完整.
收集数据
从甲、乙两个部门各随机抽取20名员工，进行了生产技能测试，测试成绩（百分制）如下：
甲 78 86 74 81 75 76 87 70 75 90
75 79 81 70 74 80 86 69 83 77
乙 93 73 88 81 72 81 94 83 77 83
80 81 70 81 73 78 82 80 70 40
整理、描述数据
按如下分数段整理、描述这两组样本数据：
成绩 人数 部门 | 40≤x≤49 | 50≤x≤59 | 60≤x≤69 | 70≤x≤79 | 80≤x≤89 | 90≤x≤100 |
甲 | 0 | 0 | 1 | 11 | 7 | 1 |
乙 |
（说明：成绩80分及以上为生产技能优秀，70--79分为生产技能良好，60--69分为生产技能合格，60分以下为生产技能不合格）
分析数据
两组样本数据的平均数、中位数、众数如下表所示：
部门 | 平均数 | 中位数 | 众数 |
甲 | 78.3 | 77.5 | 75 |
乙 | 78 | 80.5 | 81 |
