
【题目】某工厂甲、乙两个部门各有员工400人,为了解这两个部门员工的生产技能情况,进行了抽样调查,过程如下,请补充完整.
收集数据
从甲、乙两个部门各随机抽取20名员工,进行了生产技能测试,测试成绩(百分制)如下:
甲 78 86 74 81 75 76 87 70 75 90
75 79 81 70 74 80 86 69 83 77
乙 93 73 88 81 72 81 94 83 77 83
80 81 70 81 73 78 82 80 70 40
整理、描述数据
按如下分数段整理、描述这两组样本数据:
成绩 人数 部门 | 40≤x≤49 | 50≤x≤59 | 60≤x≤69 | 70≤x≤79 | 80≤x≤89 | 90≤x≤100 |
甲 | 0 | 0 | 1 | 11 | 7 | 1 |
乙 |
(说明:成绩80分及以上为生产技能优秀,70--79分为生产技能良好,60--69分为生产技能合格,60分以下为生产技能不合格)
分析数据
两组样本数据的平均数、中位数、众数如下表所示:
部门 | 平均数 | 中位数 | 众数 | |||
甲 | 78.3 | 77.5 | 75 | |||
乙 | 78 | 80.5 | 81 |
成绩 人数 部门 |
|
|
|
|
|
|
甲 | 0 | 0 | 1 | 11 | 7 | 1 |
乙 | 1 | 0 | 0 | 7 | 10 | 2 |
a.估计乙部门生产技能优秀的员工人数为400×![]() =240(人);
=240(人);
b.答案不唯一,言之有理即可.
可以推断出甲部门员工的生产技能水平较高,理由如下:
①甲部门生产技能测试中,测试成绩的平均数较高,表示甲部门生产技能水平较高;
可以推断出乙部门员工的生产技能水平较高,理由如下:
①乙部门生产技能测试中,测试成绩的中位数较高,表示乙部门生产技能水平优秀的员工较多;
②乙部门生产技能测试中,测试成绩的众数较高,表示乙部门生产技能水平较高.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=9,AC=6,BC=12,点M在AB边上,且AM=3,过点M作直线MN与AC边交于点N,使截得的三角形与原三角形相似,则MN=__.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法错误的是( )
A. 一次函数y=﹣2x+3,y随x的增大而减小,
B. 反比例函数![]() 中,y随x的增大而增大,
中,y随x的增大而增大,
C. 抛物线y=x2+1与y=x2﹣1的形状相同,只是位置不同,
D. 二次函数y=﹣2(x﹣2)2+3中,当x>2时,y随x的增大而减小
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,在△ABC中,AB=AC,点D、点O分别为BC、AC的中点,AE//BC.
(1)如图1,求证:四边形ADCE是矩形;
(2)如图2,若点 F是 CE上一动点,在不添加任何辅助线的情况下,请直接写出与四边形 ABDF 面积相等的三角形和四边形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,边AB的垂直平分线交AD于点E,交CB的延长线于点F,连接AF,BE.
(1)求证:△AGE≌△BGF;
(2)试判断四边形AFBE的形状,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,在四边形ABCD中,AD∥BC,AB∥DC,点E在BC延长线上,连接DE,∠A+∠E=180°.
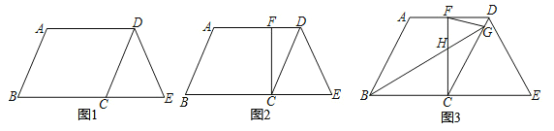
(1)如图1,求证:CD=DE;
(2)如图2,过点C作BE的垂线,交AD于点F,请直接写出BE、AF、DF 之间的数量关系_______________________;
(3)如图3,在(2)的条件下,∠ABC的平分线,交CD于G,交CF于H,连接FG,若∠FGH=45°,DF=8,CH=9,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】赵爽弦图是由四个全等的直角三角形与中间的一个小正方形拼成的一个大正方形,如图所示,若这四个全等直角三角形的两条直角边分别平行于x轴和y轴,大正方形的顶点B1、C1、C2、C3、…、Cn在直线y=﹣![]() 上,顶点D1、D2、D3、…、Dn在x轴上,则第n个阴影小正方形的面积为__.
上,顶点D1、D2、D3、…、Dn在x轴上,则第n个阴影小正方形的面积为__.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:小刚站在河边的![]() 点处,在河的对面(小刚的正北方向)的
点处,在河的对面(小刚的正北方向)的![]() 处有一电线塔,他想知道电线塔离他有多远,于是他向正西方向走了30步到达一棵树
处有一电线塔,他想知道电线塔离他有多远,于是他向正西方向走了30步到达一棵树![]() 处,接着再向前走了30步到达
处,接着再向前走了30步到达![]() 处,然后他左转
处,然后他左转![]() 直行,当小刚看到电线塔、树与自己现处的位置
直行,当小刚看到电线塔、树与自己现处的位置![]() 在一条直线时,他共走了140步.
在一条直线时,他共走了140步.
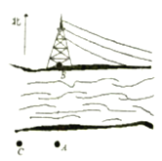
(1)根据题意,画出示意图;
(2)如果小刚一步大约50厘米,估计小刚在点![]() 处时他与电线塔的距离,并说明理由.
处时他与电线塔的距离,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com