
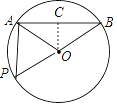
【题目】如图,已知AB是⊙O的弦,半径OA=2cm,∠AOB=120°

(1)求tan∠OAB的值;
(2)求图中阴影部分的面积S;
(3)在⊙O上一点P从A点出发,沿逆时针方向运动一周,回到点A,在点P的运动过程中,满足S△POA=S△AOB时,直接写出P点所经过的弧长(不考虑点P与点B重合的情形).
【答案】(1)![]() ;(2)(
;(2)(![]() π﹣
π﹣![]() )cm2;(3)P点所经过的弧长为
)cm2;(3)P点所经过的弧长为 ![]() πcm或
πcm或![]() πcm或
πcm或![]() πcm.
πcm.
【解析】试题分析:(1)、根据等腰三角形的性质求出∠OAB的角度,从而根据特殊角的三角函数值求出它的值;(2)、阴影部分的面积等于扇形AOB的面积减去△OAB的面积;(3)、本题需要分∠AOP=60°、∠AOP=120°和点P在弧AB上三种情况来分别进行计算,得出答案.
试题解析:(1)、解:∵OA=OB, ∴∠OAB=∠OBA,
∵∠OAB= ![]() (180°﹣120°)=30°, ∴tan∠OAB=tan30°=
(180°﹣120°)=30°, ∴tan∠OAB=tan30°=![]() ;
;
(2)、解:作OC⊥AB于C,如图,则AC=BC,
在Rt△OAC中,OC=![]() OA=1,AC=
OA=1,AC=![]() OC=
OC=![]() , ∴AB=2AC=2
, ∴AB=2AC=2![]() ,
,
∴S弓形AB=S扇形AOB﹣S△AOB=![]() ﹣
﹣![]() 2
2![]() 1=(
1=(![]() π﹣
π﹣![]() )cm2;
)cm2;
(3)、解:延长BO交⊙O于P, ∵OP=OB, ∴此时S△AOP=S△AOB,
∵∠AOP=∠OAB+∠OBA=60°, ∴此时P点所经过的弧长=![]() π(cm);
π(cm);
当点P在弧AB上,且∠AOP=60°时,时S△AOP=S△AOB ,
此时P点所经过的弧长=2π2﹣![]() π=
π=![]() π(cm);
π(cm);
当∠AOP=120时,S△AOP=S△AO, ∴此时P点所经过的弧长=![]() π(cm);
π(cm);
综上所述,P点所经过的弧长为![]() πcm或
πcm或![]() πcm或
πcm或![]() πcm.
πcm.


科目:初中数学 来源: 题型:
【题目】“龟兔赛跑”的故事同学们非常熟悉,图中的线段OD和折线OABC表示“龟兔赛跑”时路程与时间的关系,请你根据图中给出的信息,解决下列的问题:
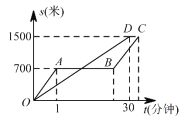
(1)折线OABC表示赛跑过程中__________(填“兔子”或“乌龟”)的路程与时间的关系,赛跑的全程是_________米;
(2)乌龟用了多少分钟追上正在睡觉的兔子?
(3)兔子醒来,以400米/分的速度跑向终点,结果还是比乌龟晚到了0.5分钟,请你计算兔子中间睡觉用了多少分钟?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场柜台销售每台进价分别为160元、120元的![]() 、
、![]() 两种型号的电器,下表是近两周的销售情况:
两种型号的电器,下表是近两周的销售情况:
销售时段 | 销售数量 | 销售收入 | |
|
| ||
第一周 | 3台 | 4台 | 1200元 |
第二周 | 5台 | 6台 | 1900元 |
(进价、售价均保持不变,利润=销售收入—进货成本)
(1)求![]() 、
、![]() 两种型号的电器的销售单价;
两种型号的电器的销售单价;
(2)若商场准备用不多于7500元的金额再采购这两种型号的电器共50台,求![]() 种型号的电器最多能采购多少台?
种型号的电器最多能采购多少台?
(3)在(2)中商场用不多于7500元采购这两种型号的电器共50台的条件下,商场销售完这50台电器能否实现利润超过1850元的目标?若能,请给出相应的采购方案;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列内容,并答题:我们知道,计算n边形的对角线条数公式为: ![]() n(n﹣3).
n(n﹣3).
如果一个n边形共有20条对角线,那么可以得到方程![]() n(n﹣3)=20 .
n(n﹣3)=20 .
整理得n2﹣3n﹣40=0;解得n=8或n=﹣5
∵n为大于等于3的整数,∴n=﹣5不合题意,舍去.
∴n=8,即多边形是八边形.
根据以上内容,问:
(1)若一个多边形共有14条对角线,求这个多边形的边数;
(2)A同学说:“我求得一个多边形共有10条对角线”,你认为A同学说法正确吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
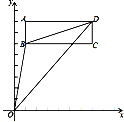
【题目】如图,在长方形ABCD中,点A(1,8),B(1,6),C(7,6).
(1)请直接写出点D的坐标;
(2)连接线段OB,OD,BD,请求出△OBD的面积;
(3)若长方形ABCD以每秒1个单位长度的速度向下运动,设运动的时间为t秒,是否存在某一时刻,使△OBD的面积与长方形ABCD的面积相等?若存在,请求出t的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图直线l1的解析式为y=x+1,直线l2的解析式为y=ax+b(a≠0);这两个图象交于y轴上一点C,直线l2与x轴的交点B(2,0)
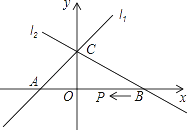
(1)求a、b的值;
(2)过动点Q(n,0)且垂直于x轴的直线与l1、l2分别交于点M、N都位于x轴上方时,求n的取值范围;
(3)动点P从点B出发沿x轴以每秒1个单位长的速度向左移动,设移动时间为t秒,当△PAC为等腰三角形时,直接写出t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB∥CD,EG、EM、FM分别平分∠AEF,∠BEF,∠EFD,则下列结论正确的有( )
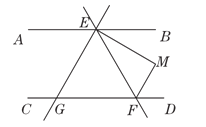
①∠DFE=∠AEF;②∠EMF=90°;③EG∥FM;④∠AEF=∠EGC.
A. 1个B. 2个
C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明用12元买软面笔记本,小丽用21元买硬面笔记本.
(1)已知每本硬面笔记本比软面笔记本贵1.2元,小明和小丽能买到相同数量的笔记本吗?
(2)已知每本硬面笔记本比软面笔记本贵a元,是否存在正整数a,使得每本硬面笔记本、软面笔记本的价格都是正整数,并且小明和小丽能买到相同数量的笔记本?若存在,求出a的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
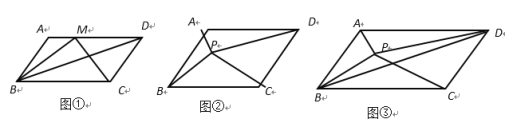
【题目】我们知道:平行四边形的面积=(底边)×(这条底边上的高).如图,四边形ABCD都是平行四边形,AD∥BC,AB∥CD,设它的面积为S.
(1)如图①,点M为AD上任意一点,若△BCM的面积为S1,则S1:S= ;
(2)如图②,点P为平行四边形ABCD内任意一点时,记△PAB的面积为Sˊ,△PCD的面积为S〞,平行四边形ABCD的面积为S,猜想得Sˊ、S〞的和与S的数量关系式为 ;
(3)如图③,已知点P为平行四边形ABCD内任意一点,△PAB的面积为3,△PBC的面积为7,求△PBD的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com