
����Ŀ����֪����ͼֱ��l1�Ľ���ʽΪy=x+1��ֱ��l2�Ľ���ʽΪy=ax+b��a��0����������ͼ����y����һ��C��ֱ��l2��x��Ľ���B��2��0��
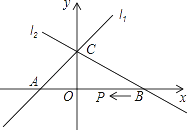
��1����a��b��ֵ��
��2��������Q��n��0���Ҵ�ֱ��x���ֱ����l1��l2�ֱ��ڵ�M��N��λ��x���Ϸ�ʱ����n��ȡֵ��Χ��
��3������P�ӵ�B������x����ÿ��1����λ�����ٶ������ƶ������ƶ�ʱ��Ϊt�룬����PACΪ����������ʱ��ֱ��д��t��ֵ��
���𰸡���1��a=��![]() ����2����1��n��2����3������������ʱ��tΪ1s��2s����3+
����2����1��n��2����3������������ʱ��tΪ1s��2s����3+![]() ����3��
����3��![]() ��s��
��s��
�����������������(1)���������������C�����꣬Ȼ��C�͵�B���������ֱ�߽���ʽ���a��b��ֵ��(2)�����������֪��Q�ڵ�A�͵�B֮�䣬�Ӷ����n��ȡֵ��Χ��(3)��������Ҫ�ּ�������ֱ������м��㣬��AC=P1C��P2A=P2C��AP3=AC��������ֱ���м���ó�t��ֵ��
���������(1)���⣺�ߵ�C��ֱ��l1��y=x+1����Ľ��㣬 ��C��0��1����
�ߵ�C��ֱ��l2�ϣ� ��b=1�� ��ֱ��l2�Ľ���ʽΪy=ax+1�� �ߵ�B��ֱ��l2�ϣ�
��2a+1=0�� ��a=��![]() ��
��
(2)���⣺�ɣ�1��֪��l1�Ľ���ʽΪy=x+1����y=0�� ��x=��1��
��ͼ��֪����Q�ڵ�A��B֮�䣬 ����1��n��2
(3)���⣺��ͼ��
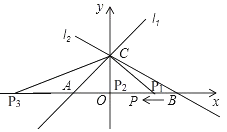
�ߡ�PAC�ǵ��������Σ� ������x����������ʱ����AC=P1Cʱ��
��CO��x�ᣬ ��OP1=OA=1�� ��BP1=OB��OP1=2��1=1�� ��1��1=1s��
����P2A=P2Cʱ����֪��P2��O�غϣ� ��BP2=OB=2�� ��2��1=2s��
����P��x�Ḻ����ʱ��AP3=AC�� ��A����1��0����C��0��1���� ��AC=![]() �� ��AP3=
�� ��AP3=![]() ��
��
��BP3=OB+OA+AP3=3+![]() ��BP3=OB+OA��AP3=3��
��BP3=OB+OA��AP3=3��![]() ��
��
����3+![]() ����1=��3+
����1=��3+![]() ��s����3��
��s����3��![]() ����1=��3��
����1=��3��![]() ��s��
��s��
��������������ʱ��tΪ1s��2s����3+![]() ����3��
����3��![]() ��s��
��s��


 �ٷ�ѧ����ҵ��������ϵ�д�
�ٷ�ѧ����ҵ��������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ���ִ�����8ʱ�ӵ�A���������������С��P���ִ��ı�ƫ��15�������ִ�ÿСʱ����15���11ʱ�ִ������B����С��P��ʱ���ִ��ı�ƫ��30������
��1�����ʱ�ִ���С��Ϊ���ٺ��
��2����С��P����Χ20���ﷶΧ���а���������ִ����ı䷽�������ǰ���У��Ƿ���д���Σ�գ���˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��������OM��CN�����߶�AB�������˵�A��B�ֱ�������OM��CN�ϣ��ҡ�C =��OAB =108�㣬F�����߶�CB�ϣ�OBƽ�֡�AOF��OEƽ�֡�COF.
(1)����ͼ���ҳ����AOC��ȵĽǣ���˵�����ɣ�
(2)��ƽ��AB����ô��OBC���OFC�Ķ������Ƿ�����ABλ�ñ仯���仯�����仯���ҳ��仯���ɣ������䣬��������ֵ.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪AB�ǡ�O���ң��뾶OA=2cm����AOB=120��

��1����tan��OAB��ֵ��
��2����ͼ����Ӱ���ֵ����S��
��3���ڡ�O��һ��P��A�����������ʱ�뷽���˶�һ�ܣ��ص���A���ڵ�P���˶������У�����S��POA=S��AOBʱ��ֱ��д��P���������Ļ����������ǵ�P���B�غϵ����Σ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����κ���y=![]() +bx+c��a��0���Ķ���ΪP����ͼ����x������������A����m��0����B��1��0������y���ڵ�C��0����3am+6a��������˵������m=3��������APB=120��ʱ��a=
+bx+c��a��0���Ķ���ΪP����ͼ����x������������A����m��0����B��1��0������y���ڵ�C��0����3am+6a��������˵������m=3��������APB=120��ʱ��a=![]() ��������APB=120��ʱ���������ϴ��ڵ�M��M��P���غϣ���ʹ����ABM�Ƕ���Ϊ120��ĵ��������Σ����������ϴ��ڵ�N������ABNΪֱ��������ʱ����a��
��������APB=120��ʱ���������ϴ��ڵ�M��M��P���غϣ���ʹ����ABM�Ƕ���Ϊ120��ĵ��������Σ����������ϴ��ڵ�N������ABNΪֱ��������ʱ����a��![]() .��ȷ���ǣ� ��.
.��ȷ���ǣ� ��.
A���٢� B���ۢ� C���٢ڢ� D���٢ڢۢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ�κ���y=mx+4��ͼ����x���ཻ�ڵ�A���뷴��������y=![]() ��x>0����ͼ���ཻ�ڵ�B��1��6����
��x>0����ͼ���ཻ�ڵ�B��1��6����
��1����һ�κ����ͷ����������Ľ���ʽ��
��2�����P��x����һ�㣬��S��APB=18��ֱ��д����P�����꣮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ƽ���ı���ABCD�У�AB��AC��AB=2��AC=4���Խ���AC��BD�ཻ�ڵ�O����ֱ��AC�Ƶ�O˳ʱ����ת![]() ����0����
����0����![]() ��180����������ֱ��BC��AD�ڵ�E��F��
��180����������ֱ��BC��AD�ڵ�E��F��

��1����![]() =_____��ʱ���ı���ABEF��ƽ���ı��Σ�
=_____��ʱ���ı���ABEF��ƽ���ı��Σ�
��2������ת�Ĺ����У���A��B��C��D��E��F������4����Ϊ���㹹���ı��Σ�
�ٵ�![]() =_______��ʱ��������ı��������Σ�
=_______��ʱ��������ı��������Σ�
����������ı����Ǿ��Σ���þ��ε����߳���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ƻ�������ͼ��ʾ�ľ����߲�������Ҫ���ı�Ϊ3��1��������������ǰ���������ǽ����2.5m���Ŀյط��ù���������������ǽ����1m����ͨ�����м���������1m����ͨ����ͨ����ǰ��ǽƽ����ʣ��յأ���Ӱ���֣�Ϊ��ֲ��������ֲ�������300m2����������ҵij�����Ƕ��٣�
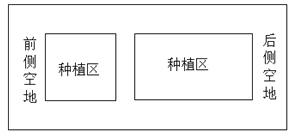
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com