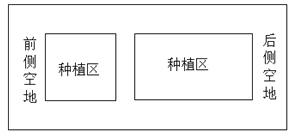
【题目】某村计划建造如图所示的矩形蔬菜温室，要求长宽的比为3：1，在温室内，沿前后两侧的内墙各留2.5m宽的空地放置工具，其他两侧内墙各留1m宽的通道．中间区域再留1m宽的通道，通道与前后墙平行，剩余空地（阴影部分）为种植区，当种植区面积是300m2，求矩形温室的长与宽是多少？
名校课堂系列答案科目：初中数学 来源： 题型：
【题目】已知，如图直线l1的解析式为y=x+1，直线l2的解析式为y=ax+b（a≠0）；这两个图象交于y轴上一点C，直线l2与x轴的交点B（2，0）
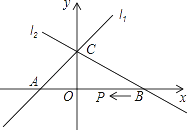
（1）求a、b的值；
（2）过动点Q（n，0）且垂直于x轴的直线与l1、l2分别交于点M、N都位于x轴上方时，求n的取值范围；
（3）动点P从点B出发沿x轴以每秒1个单位长的速度向左移动，设移动时间为t秒，当△PAC为等腰三角形时，直接写出t的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】等腰Rt△ACB，∠ACB＝90°，AC＝BC，点A、C分别在x轴、y轴的正半轴上．
（1）如图1，求证：∠BCO＝∠CAO
（2）如图2，若OA＝5，OC＝2，求B点的坐标
（3）如图3，点C（0，3），Q、A两点均在x轴上，且S△CQA＝18．分别以AC、CQ为腰在第一、第二象限作等腰Rt△CAN、等腰Rt△QCM，连接MN交y轴于P点，OP的长度是否发生改变？若不变，求出OP的值；若变化，求OP的取值范围．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】抛物线y=ax2+bx+c交x轴于A、B两点，交y轴于点C,已知抛物线的对称轴为x=1，B(3,0),C(0,-3)，
（1）求二次函数y=ax2+bx+c的解析式；
（2）在抛物线对称轴上是否存在一点P，使点P到B、C两点距离之差最大？若存在，求出P点坐标；若不存在，请说明理由；
（3）平行于x轴的一条直线交抛物线于M,N两点，若以MN为直径的圆恰好与x轴相切，求此圆的半径．
查看答案和解析>>
科目：初中数学 来源： 题型：
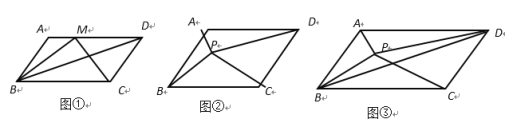
【题目】我们知道：平行四边形的面积＝(底边)×(这条底边上的高)．如图，四边形ABCD都是平行四边形，AD∥BC，AB∥CD，设它的面积为S．
（1）如图①，点M为AD上任意一点，若△BCM的面积为S1，则S1：S＝ ；
（2）如图②，点P为平行四边形ABCD内任意一点时，记△PAB的面积为Sˊ，△PCD的面积为S〞，平行四边形ABCD的面积为S，猜想得Sˊ、S〞的和与S的数量关系式为 ；
（3）如图③，已知点P为平行四边形ABCD内任意一点，△PAB的面积为3，△PBC的面积为7，求△PBD的面积．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】阅读下列材料：
“ a 2 ≥0”这个结论在数学中非常有用，有时我们需要将代数式配成完全平方式．例如：
x2 4x 5 x2 4x 4 1 x 22 1 ，
∵ x 22 ≥0，
∴ x 22 1 ≥1，
∴ x2 4x 5 ≥1.
试利用“配方法”解决下列问题：
(1)填空： x2 4x 5 ( x )2＋ ；
(2)已知 x2 4x y2 2y 5 0 ，求 x y 的值；
(3)比较代数式 x2 1与2x 3 的大小．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】为了贯彻落实区中小学“阅读·写字·演讲”三项工程工作，我区各校大力推广阅读活动，某校初二（1）班为了解2月份全班学生课外阅读的情况，调查了全班学生2月份读书的册数，并根据调查结果绘制了如下不完整的条形统计图和扇形统计图：
根据以上信息解决下列问题：
（1）参加本次问卷调查的学生共有______人，其中2月份读书2册的学生有______人；
（2）补全条形统计图，并求扇形统计图中读书3册所对应扇形的圆心角度数．
查看答案和解析>>
科目：初中数学 来源： 题型：
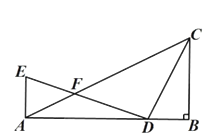
【题目】如图，在△ABC中，∠ABC＝90°，D为AB边上一点（BD＜BC），AE⊥AB，AE＝BD，连接DE交AC于F，若∠AFE＝45°，AD＝3
，CD＝5，则线段AC的长度为_________．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
