
【题目】如图,正方形![]() 的面积为4,点
的面积为4,点![]() ,
,![]() 分别是
分别是![]() ,
,![]() 的中点,将点
的中点,将点![]() 折到
折到![]() 上的点
上的点![]() 处,折痕为
处,折痕为![]() ,点
,点![]() 在
在![]() 上,则
上,则![]() 长为___.
长为___.
【答案】![]()
【解析】
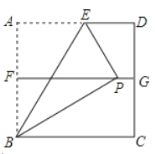
利用正方形ABCD的面积为4得到正方形ABCD的边长为2,再根据折叠的性质得BA=BP=2,∠ABE=∠PBE;由于点F,G分别是AB,DC的中点,则FG⊥AB,BF=1,在Rt△BPF中,由于PB=4,BF=2,根据含30度的直角三角形三边的关系得到得到∠FPB=30°,利用互余得∠ABP=60°,则∠ABE=30°,然后在Rt△ABE中根据含30度的直角三角形三边的关系求AE的长.
∵正方形ABCD的面积为4,
∴正方形ABCD的边长为2,
∵点A折到FG上的点P处,折痕为BE,
∴BA=BP=2,∠ABE=∠PBE,
∵点F,G分别是AB,DC的中点,
∴FG⊥AB,BF=1,
在Rt△BPF中,PB=2,BF=1,
∴∠FPB=30°,
∴∠ABP=60°,
∴∠ABE=30°,
在Rt△ABE中,
![]() .
.
故填:![]() .
.


 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案科目:初中数学 来源: 题型:
【题目】二次函数y=![]() +bx+c(a>0)的顶点为P,其图象与x轴有两个交点A(﹣m,0),B(1,0),交y轴于点C(0,﹣3am+6a),以下说法:①m=3;②当∠APB=120°时,a=
+bx+c(a>0)的顶点为P,其图象与x轴有两个交点A(﹣m,0),B(1,0),交y轴于点C(0,﹣3am+6a),以下说法:①m=3;②当∠APB=120°时,a=![]() ;③当∠APB=120°时,抛物线上存在点M(M与P不重合),使得△ABM是顶角为120°的等腰三角形;④抛物线上存在点N,当△ABN为直角三角形时,有a≥
;③当∠APB=120°时,抛物线上存在点M(M与P不重合),使得△ABM是顶角为120°的等腰三角形;④抛物线上存在点N,当△ABN为直角三角形时,有a≥![]() .正确的是( ).
.正确的是( ).
A.①② B.③④ C.①②③ D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知ABC在平面直角坐标系内,满足:点A在y轴正半轴上移动,点B在x轴负半轴上移动,点C为y轴右侧一动点.

点A0,a和点Bb,0坐标恰好满足:![]() ,直接写出a,b的值.
,直接写出a,b的值.
⑵如图①,当点C在第四象限时,若AM、AO将BAC三等分,BM、BO将ABC三等分,在A、B、C的运动过程中,试求出C和M的关系.
⑶探究:
(i)如图②,当点C在第四象限时,若AM平分CAO,BM平分CBO,在A、B、C的运动过程中,C和M是否存在确定的数量关系?若存在,请证明你的结论;若不存在,请说明理由.
(ii)如图③,当点C在第一象限时,且在(i)中的条件不变的前提下,C和M又有何数量关系?证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,丁轩同学在晚上由路灯AC走向路灯BD,当他走到点P时,发现身后他影子的顶部刚好接触到路灯AC的底部,当他向前再步行20m到达Q点时,发现身前他影子的顶部刚好接触到路灯BD的底部,已知丁轩同学的身高是1.5m,两个路灯的高度都是9m,则两路灯之间的距离是( )

A. 24m B. 25m C. 28m D. 30m
查看答案和解析>>
科目:初中数学 来源: 题型:
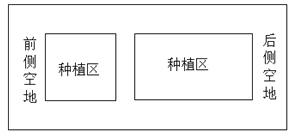
【题目】某村计划建造如图所示的矩形蔬菜温室,要求长宽的比为3:1,在温室内,沿前后两侧的内墙各留2.5m宽的空地放置工具,其他两侧内墙各留1m宽的通道.中间区域再留1m宽的通道,通道与前后墙平行,剩余空地(阴影部分)为种植区,当种植区面积是300m2,求矩形温室的长与宽是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明和妈妈购物后回家,在一楼电梯口看到电梯正显示在顶楼(9楼),他们等了18s后,电梯显示在7楼,这时小明选择走楼梯,高度上升的速度为![]() ,他妈妈则继续等电梯,结果两个人同时到达家所在的楼层。图中所示的细线、粗线分别表示电梯匀速升降、小明走楼梯与一楼地面的距离h(m)与时间t(s)之间的关系。(温馨提示:小明家所在的电梯楼房为3m一层,人们进出电梯所用时间忽略不计,楼层与楼高的关系).
,他妈妈则继续等电梯,结果两个人同时到达家所在的楼层。图中所示的细线、粗线分别表示电梯匀速升降、小明走楼梯与一楼地面的距离h(m)与时间t(s)之间的关系。(温馨提示:小明家所在的电梯楼房为3m一层,人们进出电梯所用时间忽略不计,楼层与楼高的关系).

(1)写出A,B两点的坐标;
(2)写出直线AB的解析式,并解释点C的实际意义;
(3)求a,b的值,并求出小明家所处的楼层.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】教室里的饮水机接通电源就进入自动程序,开机加热时每分钟上升10℃,加热到100℃,停止加热,水温开始下降,此时水温(℃)与开机后用时(min)成反比例关系.直至水温降至30℃,饮水机关机.饮水机关机后即刻自动开机,重复上述自动程序.若在水温为30℃时,接通电源后,水温y(℃)和时间(min)的关系如图,为了在上午第一节下课时(8:45)能喝到不超过50℃的水,则接通电源的时间可以是当天上午的( )

A.7:20 B.7:30 C.7:45 D.7:50
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,延长平行四边形ABCD的边DC到点E,使CE=DC,连接AE,交BC于点F,连接AC、BE.
(1)求证:BF=CF;
(2)若AB=2,AD=4,且∠AFC=2∠D,求平行四边形ABCD的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,观察由棱长为 ![]() 的小立方体摆成的图形,寻找规律:如图 ① 中,共有
的小立方体摆成的图形,寻找规律:如图 ① 中,共有 ![]() 个小立方体,其中
个小立方体,其中 ![]() 个看得见,
个看得见, ![]() 个看不见;如图 ② 中,共有
个看不见;如图 ② 中,共有 ![]() 个小立方体,其中
个小立方体,其中 ![]() 个看得见,
个看得见, ![]() 个看不见;如图 ③ 中,共有
个看不见;如图 ③ 中,共有 ![]() 个小立方体,其中
个小立方体,其中 ![]() 个看得见,
个看得见, ![]() 个看不见;
个看不见; ![]() ,则第 ⑥个图中,看得见的小立方体有________________个.
,则第 ⑥个图中,看得见的小立方体有________________个.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com